Fourier Transform

Abstract:

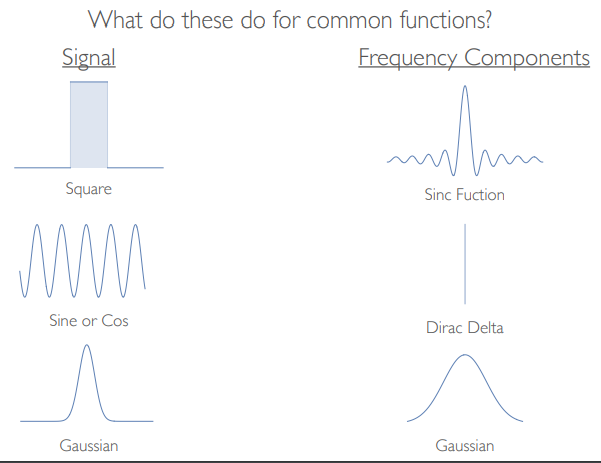
In general it’s very easy to use Fourier Series to represent our waves as a combination of sine and cosine waves for [[Periodic Functions|Periodic Functions]] however we come to find that for non periodic functions, our fourier series begins to present us with some awful looking formulas.

Fortunately fourier himself provided us a solution to this, with his Fourier Transforms, which convert these complicated functions into their constituent waves

Formula:

$$f(\omega )={\int }_{\infty }^{\infty }f(t)e^{-2i\pi \omega t}dt$$

Discrete Fourier Transform:

As fourier transform is done over bound $-\infty$ to $\infty$ we can only do it over continous waves, however most of the time we’d like to do a Fourier Transform over finite discrete bounds, so we use Discrete Fourier Transform (DFT):

$$F_K=\sum _{n=0}^{N-1}{f}_n\ast e^{-\frac{2i\pi kn}{N}}$$

Where n is the position of the bit for example, and N is the length of the data being sampled Note :

$$e^{-\frac{2i\pi kn}{N}}=\cos (\frac{2i\pi kn}{N})-i\sin (\frac{2i\pi kn}{N})$$

Ex:

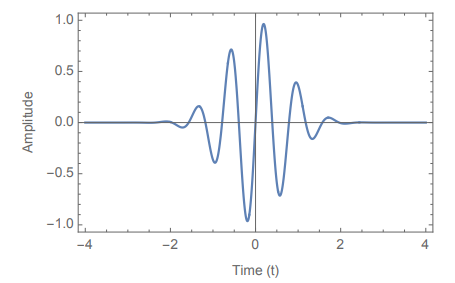Gives us: 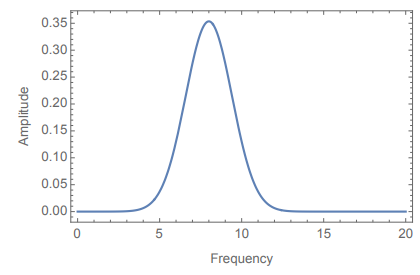Which roughly means:

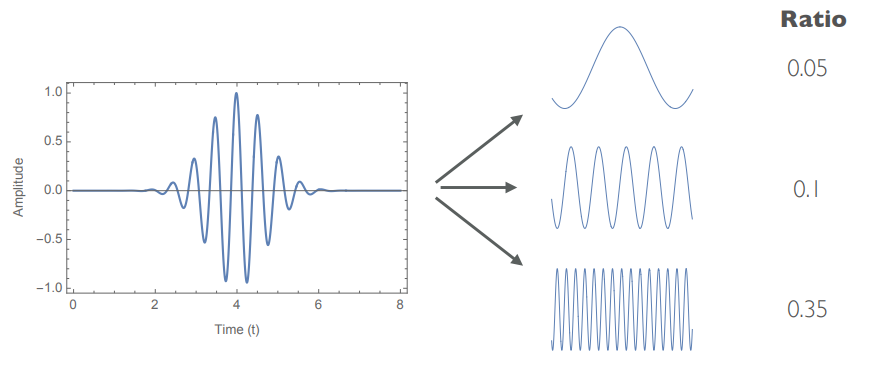
General Forms: