ESD Block 2 Sheet

Electronic System Design 3

Practical Questions:

Resistor Error %

General Formula:

$$\begin{array}{rl}\frac{V_{cm}}{V_{Diff}}& =\frac{2Ra+R_B}{R_B}/\frac{2\rho }{R}\\ & =\frac{2Ra+R_B}{R_B}\ast \frac{R}{2\rho }\\ & =\frac{R\ast A_v}{2\rho }\\ \frac{V_{diff}}{V_{cm}}& =\frac{2\rho }{R\ast A_v}\\ & =\frac{2}{A_v}\ast \frac{\rho }{R}\\ \therefore \frac{\rho }{R}& =\frac{V_{diff}\ast A_v}{2\ast V_{cm}}\end{array}$$

Example

Abstract

Given you have calculated the Total CMRR of an Instrumental Amplifier to be $80dB$, and you know you need $34dB$ of CMRR in your Output Stage, calculate the tolerance of the resistors in the output stage. Your Common Mode Voltage is $5V$, and your Differential Voltage is $500\mu V$

Example

\begin{align} \text{We know that: }\\ Av*V_{diff} &\geq A_{cm}*V_{cm} \\ \text{Calculate tolerance at limit:}&\\ \frac{V_{cm}}{V_{diff}} = \frac{A_v}{A_{cm}} &\equiv A_v/(\frac{2\rho}{R}) \\ \frac{V_{cm}}{V_{diff}} &= \frac{RA_v}{2\rho} \\ \therefore \frac{V_{diff}}{V_{cm}} &= \frac{2\rho}{RA_v} \\ \frac{V_{diff}}{V_{cm}} &= \frac{2}{A_v} * \frac{\rho}{R} \\ \therefore \frac{\rho}{R} &= \frac{V_{diff}*A_v}{2*V_{cm}} \\ \text{Note: Gain(dB) =} & \text{ Total CMRR - O/P CMRR} = 80-34 = 46dB \\ \frac{\rho}{R} &= \frac{500*10^{-6}*(10^{\frac{(80-34)}{20}})}{2*5} \approx 0.01 \\ \therefore \text{ Tolerance \%} &= 100 * 0.01 = 1\% \\ \end{align}

Error Analysis

For $R_B<R_T$ , Where $R_T=R_{In(+)}+R_{In(-)}$

$$\begin{array}{rl}\text{Error Budget }& =CMR{R}_{resistor}+FOM\\ & =FOM+\frac{V_{cm}\ast 2\frac{\rho }{R}}{A_v}\end{array}$$

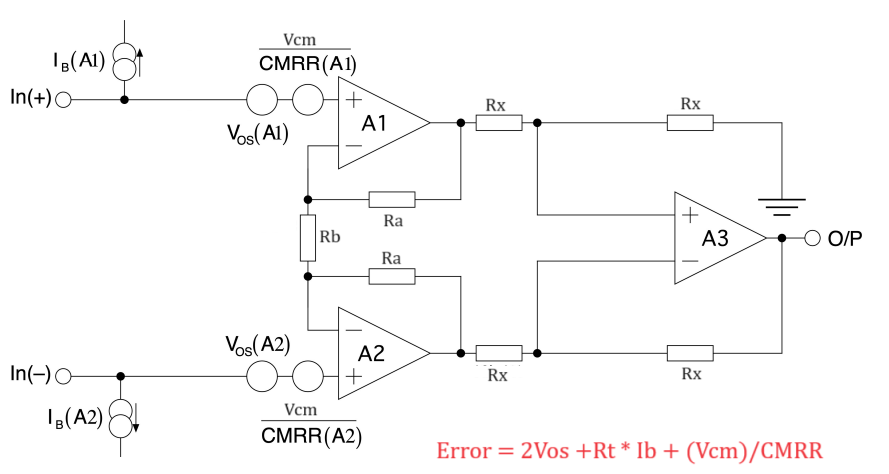
Example:

Abstract

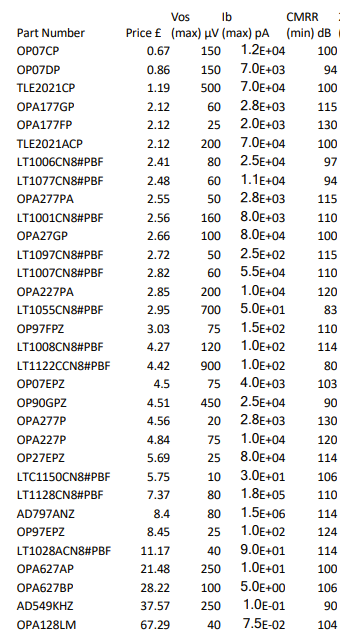
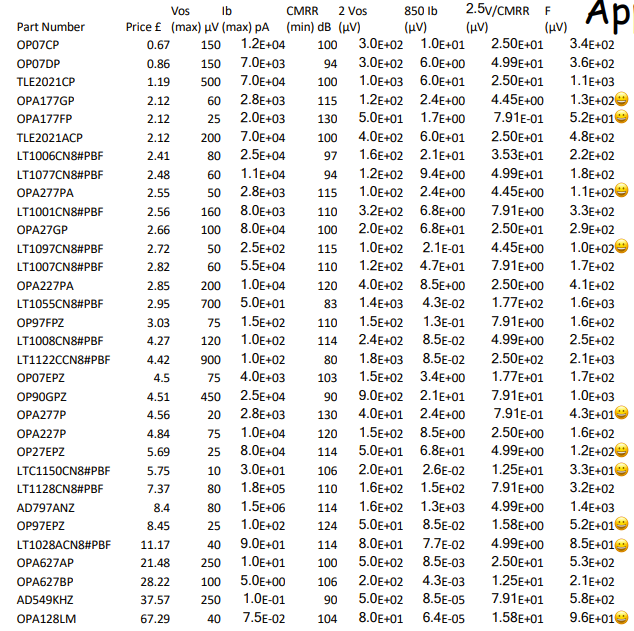
From previous questions you have deduced that your Error Budget is $218\mu V$, assuming $R_{In(+)}=R_{In(-)}=425\Omega ,V_{cm}=2.5V,A_v=80$, In addition to this you have decided on $R_A=3k9\Omega ,R_B=100\Omega ,R_x(\%)=1\%$ find the best op amp from the following table:

Example

First let’s attempt to calculate our Resistor CMRR first to see if it is suitable, as this component is seperate from Op-Amp spec, and exponentially increases in price for precision: $CMR{R}_R=\frac{2.5V\ast 2\ast 0.01}{80}=625\mu V>>218\mu V$ Resistor tolerance way too large! Try again with 0.1% $CMR{R}_R=\frac{2.5V\ast 2\ast 0.001}{80}=62.5\mu V<218\mu V$ This is a suitable error budget for our resistors. From earlier we can define our Figure of Merit as: $FOM=2V_{os}+(R_{In(+)}+R_{In(-)})\ast I_b+\frac{V_{CM}}{CMRR}$ $FOM=2V_{os}+825\ast I_b+\frac{2.5}{CMRR}$ From this we can write our FOM on the table provided looking for: $FOM<218\mu V-62.5\mu V=155.5\mu V$

Understanding Bridges

A bridge is a form of “pre-circuit” where you want to take the differential voltage for a single source, and therefore need something to compare against, 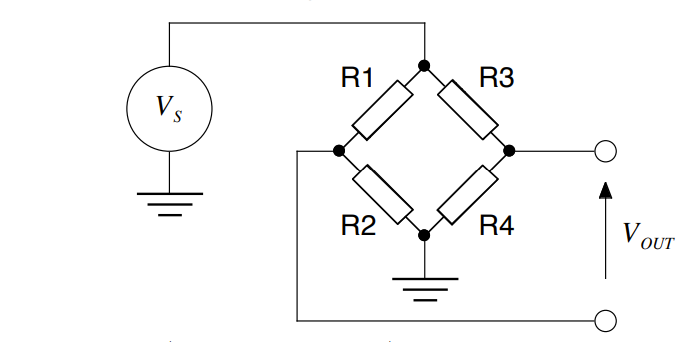Where R4 tends to be a Resistor that varies with some external factor (e.g. temperature) The variable resistor is defined by $R(1+ϵ)$, where $ϵ$ is the factor that changes with the external factor: Therefore from this $V_{out}=V_s(\frac{R_4}{R_3+R_4}-\frac{R2}{R_2+R_1})$ . If we allow $R1=R2=R3=R4(1+ϵ)$ at some level, We can define $V_{out}=V_s(\frac{1}{2+ϵ}-\frac{1}{2})$ . From here, using the binomial expansion of $(1+x{)}^{-}1\approx 1-x+x^2...$

$$V_{out}=V_s(\frac{1}{2+ϵ}-\frac{1}{2})=\frac{V_s}{2}(\frac{1}{1+(\frac{ϵ}{2})}-1)\approx \frac{V_s}{2}([1-\frac{ϵ}{2}+\frac{{ϵ}^2}{4}]-1)=V_s(-\frac{ϵ}{4}+\frac{{ϵ}^2}{8})\approx -\frac{ϵ}{4}{V}_s$$

Limit on sensitivity = CMRR:

$$\begin{array}{rl}-\frac{V_sϵ}{4}& =\frac{V_{cm}}{CMRR}=\frac{V_s/2}{CMRR}\\ \text{Sensitivity}& =\text{Min Change in }ϵ\equiv {ϵ}_{min}\\ \therefore -V_s\frac{{ϵ}_{min}}{4}& =\frac{V_s/2}{CMRR}\\ ⟹{ϵ}_{min}& =\frac{2}{CMRR}\end{array}$$

Abstract

A bridge amplifier is to be constructed to signal condition the output from a platinum resistance thermometer. The platinum resistance thermometer has a resistance proportional to absolute temperature and has a resistance of 100Ω at 0°C. The resistance therefore varies by 0.366Ω / °C near 0°C. Design an instrumentation amplifier to condition the bridge output such that the error due to common-mode rejection is less than 0.05°C. What is the error due to voltage offset in your design?

Example

With the knowledge our PT is $100\Omega$ at $0^o$, lets build our calculations around that. Let $R=100\Omega$. Now we need to define the $V_s$ of the system. So what is limiting it? Well we know that we’re using a resistance thermometer, but resistors produce their own heat under higher power. So providing too much power through our resistors will ruin the accuracy of our Resistance Thermometer, so let us limit Power to $P<1mW$, we know from our Power Rules that $P=i^{2}R$, so for this we would rearrange to $i<\sqrt{\frac{P}{R}}=\sqrt{\frac{0.01}{100}}$ so $i<3.16mA$. So with this we can attempt to find $V_s$, knowing that $V_s<2R\ast i=200\ast 3.16\ast 10^{-3}=0.632V$ so let $V_s=0.5V$
We know our LHS of the bridge will be $0.25V$, And using $R_{PT100}=100+0.366T,\therefore ϵ=\frac{0.366T}{100}$. So our RHS will be $0.5V\ast \frac{100}{100+100(1+ϵ)}=0.5V\ast (\frac{1}{2}-\frac{1}{2+ϵ})=0.5V\ast (\frac{1}{2}-\frac{1}{2}\ast \frac{1}{1+\frac{ϵ}{2}})$ $=0.5V\ast (\frac{1}{2}-\frac{1}{2}\ast (1-\frac{ϵ}{2}+\frac{{ϵ}^2}{4}))=0.5V\ast (\frac{ϵ}{4}+\frac{{ϵ}^2}{8})\approx 0.5V\ast (\frac{ϵ}{4})=0.5V\ast \frac{0.366T}{400}=4.58\ast 10^{-4}T$ (in Volts) So a sensitivity of $0.05^{o}C$ creates a differential of $0.05\ast 4.58\ast 10^{-4}=23\mu V$. So $23\mu V\ast A_v\ge 2.5V\ast A_{cm}$ and $CMRR\equiv \frac{A_v}{A_{cm}}=\frac{2.5}{23\ast 10^{-6}}=10870=80.7dB$ From here, as we haven’t been told a gain, we should choose the largest Practical gain, say an output of $100mV{/}^{o}C$ so $A_v=\frac{100x10^{-3}}{4.58\ast 10^{-4}}=218=46.8dB$. So this gives us an O/P CMRR of $80.7db-46.8dB=33.9dB$. Now as O/P CMRR = $\frac{1}{2\ast tolerance}$, we can say our tolerance is $\frac{1}{2\ast \text{O/P CMRR}}=\frac{1}{2\ast 10^{\frac{33.9}{20}}}=0.01$, so we can use 1% resistors for this purpose. So, with this in mind, for our 3 stage Instrumental Amplifier we can define $R_x=5k1$ as a sensible value, as the actual value doesn’t matter. We know our gain = $218=1+\frac{2R_a}{R_b}$ so If we select $R_b$ to be $100\Omega$, $R_a\approx 11k\Omega$. and the tolerance of those doesnt matter, let it be 1%, and we know the tolerance of the output stage must be 1% for the resistors. So: , Where the op amp has been chosen to have a CMRR >>Total Circuit CMRR, i.e >>80dB

Book Knowledge

Understanding Common Mode Gain Derivation

Maximum Asymmetry:

This is the worst case for Common Mode Gain:

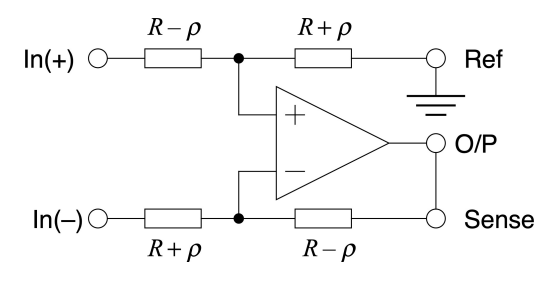
Where $\rho$ is the error in the resistor

Due to VEP we can set the voltages on both sides to be equal, therefore

$$\begin{array}{rl}{V}_{cm}+(Ref-V_{cm})\frac{R-\rho }{(R+\rho )+(R-\rho )}& =V_{cm}+(Sense-V_{cm})\frac{R+\rho }{(R+\rho )+(R-\rho )}\\ V_{cm}+(Ref-V_{cm})\frac{R-\rho }{2R}& =V_{cm}+(Sense-V_{cm})\frac{R+\rho }{2R}\end{array}$$

Output = (Sense - Ref)

$$\begin{array}{rl}(Ref-V_{cm})\frac{R-\rho }{2R}& =(Sense-V_{cm})\frac{R+\rho }{2R}\\ Ref\frac{R-\rho }{2R}-V_{cm}\frac{R-\rho }{2R}& =Sense\frac{R+\rho }{2R}-V_{cm}\frac{R+\rho }{2R}\\ Sense\frac{R+\rho }{2R}-Ref\frac{R-\rho }{2R}& =V_{cm}(\frac{R+\rho }{2R}-\frac{R-\rho }{2R})\\ & \\ \rho <& <R\\ ⟹\frac{(Sense-Ref)R}{2R}=& \frac{(Sense-Ref)}{2}\approx \frac{2\rho }{2R}\\ ⟹\text{Common Mode Gain}\equiv & \frac{(Sense-Ref)}{V_{cm}}\approx \frac{2\rho }{R}\end{array}$$

Symmetry:

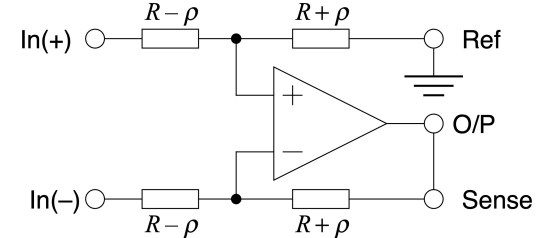Let $In(+)=In(-)=\frac{V_{diff}}{2}$

Then:

$$\begin{array}{rl}(Sense-Ref)& =V_{diff}\frac{R+\rho }{R-\rho }\\ & =V_{diff}\frac{1+\frac{\rho }{R}}{1-\frac{\rho }{R}}\\ & =V_{diff}(1+\frac{\rho }{R})(1-\frac{\rho }{R}{)}^{-1}\\ A_{diff}& =\frac{(Sense-Ref)}{V_{diff}}=(1+\frac{\rho }{R})(1-\frac{\rho }{R}{)}^{-1}\\ \text{Knowing: }& (1+x{)}^{-1}=1-x+x^2\\ \text{Hence: }& A_{diff}\approx (1+\frac{\rho }{R})(1+\frac{\rho }{R})=1+\frac{2\rho }{R}+\frac{{\rho }^2}{R^2}\\ \text{However: }& \rho <<R\text{ , so}\\ & A_{diff}\approx 1+\frac{2\rho }{R}\end{array}$$

therefore:

$$CMRR=\frac{\text{Differential Gain}}{\text{Common-Mode Gain}}=\frac{1+2\rho /R}{2\rho /R}\approx \frac{R}{2\rho }=\frac{1}{2\ast \text{Tolerance}}$$

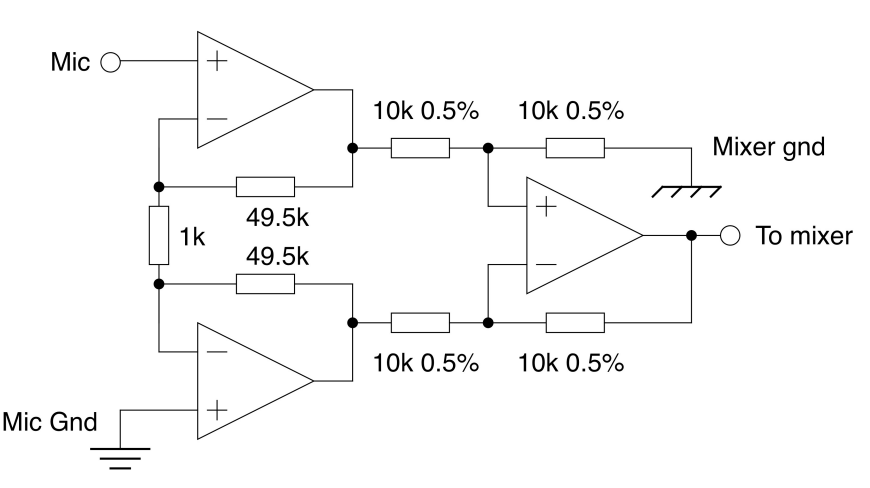
Derive Gain for 3 Op Amp Instrumental Amp

With a differential:

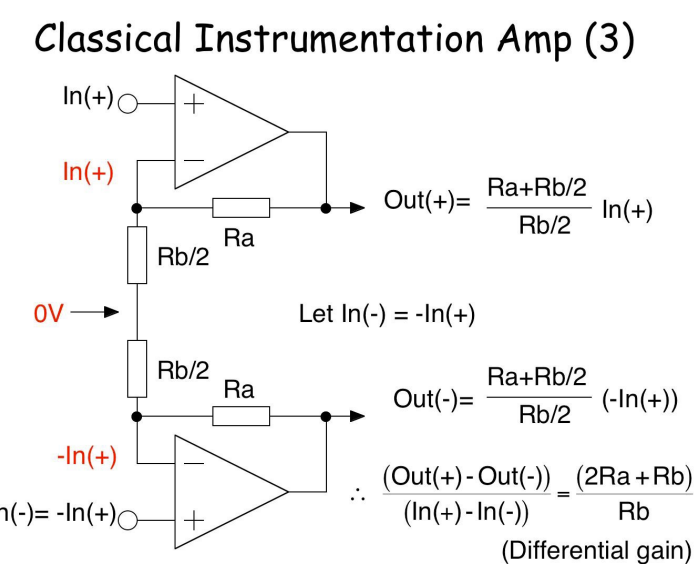
Without a differential:

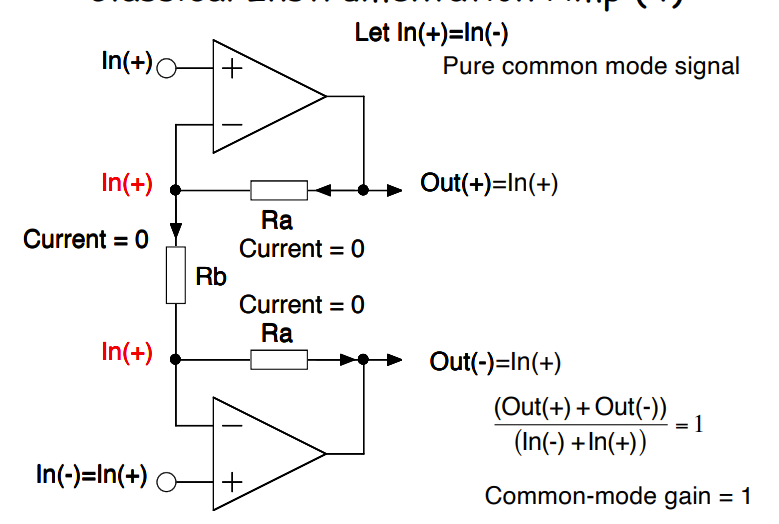
Different Power Sources:

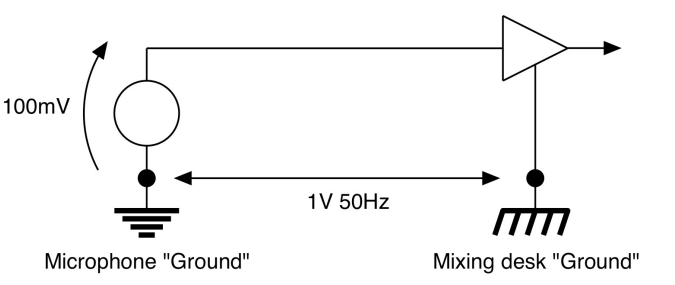
Abstract

A microphone produces an output of 100mV peak and is input to a mixing desk The ground connection used by the microphone has a 50Hz (Mains) signal of 1V amplitude on it, relative to the ground used by the mixing desk.

Example

In this example, the added amplitude of the signal (1V) is 10 times larger than the differential peak. So if we had a CMRR of 10, our signal would be at most the same amplitude of the 50Hz noise So $\text{Actual CMRR}=\frac{\text{Relative Input Amplitude}}{\text{Input Differential}}\ast \text{Desired CMRR}$ So say we wanted the microphone signal to be 1000 times larger than the 50Hz, we need a CMRR of 10000 (80dB), and if we want a 10V output from this, we would need $A_v=\frac{10}{100\ast 10^{-3}}=100$ So: $A_v=100$ $CMRR=10000$ So our O/P CMRR will be $\frac{10000}{100}=100$ So our O/P resistor tolerance shall be $\frac{1}{2\ast \text{O/P CMRR}}=1/200$ so the tolerance % is $1/2=0.5\%$ Given $R_b=100\Omega ,Ra=49k5\Omega$, and let $R_x=10k\Omega$

Pros & Cons:

Difference amplifier has problems

• Sensitivity to source impedance
• CMRR defined by (expensive) resistor tolerance

Classical 3-opamp instrumentation amplifier solves them:

• Infinite input impedance
• CMRR increased by input stage differential gain CMRR of 3-opamp instrumentation amp and gain are linked