Models

Index: Modelling, Simulation of Engineering Systems 3

A Model is the description of a System using appropriate mathematical formulation

Conceptually you can either approach a problem with more Theoretical Modelling or more Experimental Modelling.

Pure Theoretical Modelling leads to White Box Modelling, which is purely ODEs, with known parameters.

Pure Experimental Modelling leads to Black Box Modelling, which is like Neural Networks, but conceptually only the input and output are measurable, and we have to assume the structure, as we can’t actually decypher the structure. The range:

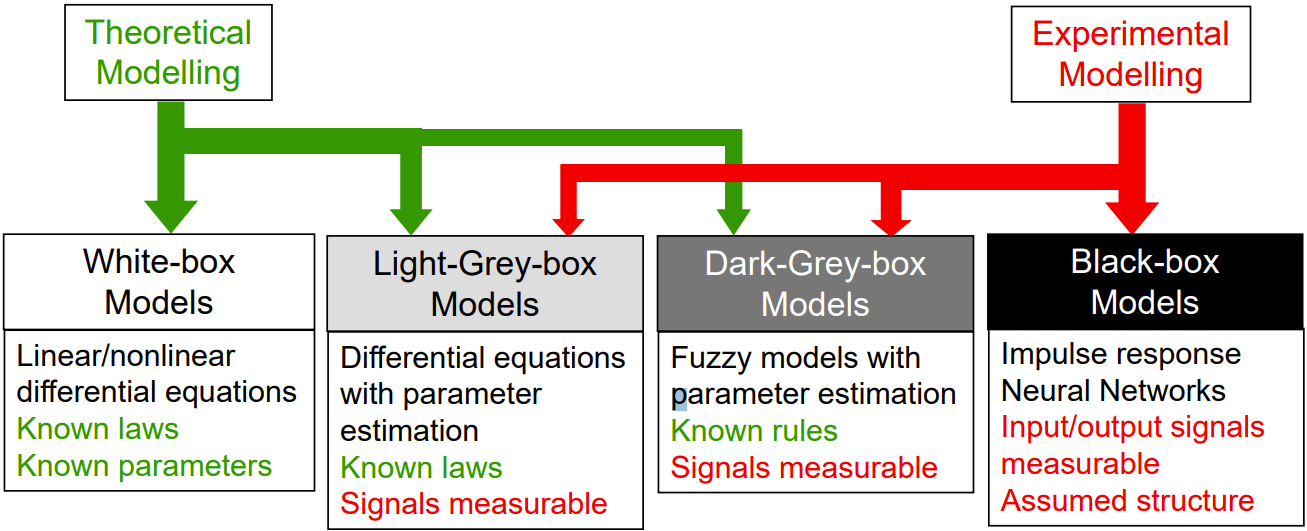
Three Types of Models:

State Space:

Nonlinear time domain representation of the system

Abstract:

The State Space Form is a set of decoupled first order Ordinary Differential Equations (ODEs) which describe the dynamics of the system. Ideally we are trying to represent the stability and general system as a matrix or matrix equation as this is most convenient for putting into MATLAB.

As state space is first order ODE, we need to convert most systems that are higher order into the correct form.

Assume that the dynamics of a system can be represented in the form

$$u(t)=f(t,y,\frac{dy}{dt},\frac{d^{2}y}{d{t}^2},...,\frac{d^{n-1}y}{d{t}^{n-1}},\frac{d^{n}y}{d{t}^n})$$

Here the input/forcing function is $u(t)$ and the main dynamic is $y$. We’d describe the system as an $N^{th}$ order system.

Approach:

The first step is to take the diff eq, and rearrange the dynamic eq into a reduced form (i.e. in terms of highest power)

$$\frac{d^{n}y}{d{t}^n}=f(t,y,\frac{dy}{dt},\frac{d^{2}y}{d{t}^2},...,\frac{d^{n-1}y}{d{t}^{n-1}},u(t))$$

\usepackage{amsmath}
 
\begin{document} \label{eq1}
\begin{equation}
\begin{align*}
x_1 &= y \\ x_2 &= \frac{dy}{dt} \\
... \\
x_n &= \frac{d^{n-1}y}{dt^{n-1}}
\end{align*}
\end{split}
\end{document}

The second step is to assign these x values to all but the highest value order

$$\begin{array}{c}{x}_1=y\\ x_2=\frac{dy}{dt}\\ ...\\ x_n=\frac{d^{n-1}y}{d{t}^{n-1}}\end{array}$$

The third step is to take the derivate of all these state variables

$$\begin{array}{c}\dot{x_1}=\frac{dy}{dt}\\ \dot{x_2}=\frac{d^{2}y}{d{t}^2}\\ ...\\ \dot{x_n}=\frac{d^{n}y}{d{t}^n}\end{array}$$

The fourth step is to subsitute state variable and the reduced form back into the derivate eq

$$\begin{array}{c}\dot{x_1}=x_2\\ \dot{x_2}=x_3\\ \dot{x_n}=f^{\prime }(t,x_1,x_2,...,x_n,u(t))\end{array}$$

General Form:

State Derivates = System Matrix * State Vector + Input Matrix * Input Vector

$$\left[\begin{array}{c}\dot{x_1}\\ \dot{x_2}\\ ...\\ \dot{x_n}\end{array}\right]=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{21}& ...\\ ...& ...& ...\\ a_{n1}& ...& ...\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]+\left[\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{21}& ...\\ ...& ...& ...\\ b_{n1}& ...& ...\end{array}\right]\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]$$

Conversion into State Space:

todo

Block Diagram:

Block based graphical representation of the system

Transfer Function:

Linear frequency domain representation of the system

Abstract:

Not used as much in continous systems, however we learn it so we know how to convert it