SES Assignment 1-LAPTOP-7ECIK81A

This is part 1 of the assignment for Simulation of Engineering Systems 3

State Space:

$$(2)L\frac{di}{dt}+Ri+K_e{\omega }_m=V_{in}$$ $$(Left)\frac{di}{dt}=\frac{1}{L}[(V_D+\Delta V)-Ri-K_e{\omega }_m]$$ $$(Right)\frac{di}{dt}=\frac{1}{L}[(V_D-\Delta V)-Ri-K_e{\omega }_m]$$

For the left hand side: $x_1=i_L$, $x_2={\omega }_m^L$, $x_3={\omega }_w^L$ , For the right hand side $x_4=i_R$, $x_5={\omega }_m^R$, $x_6={\omega }_w^R$

$$\dot{x_1}=\frac{V_o+\Delta V}{L}-\frac{R{x}_1}{L}-\frac{K_e{x}_2}{L}$$ $$\dot{x_4}=\frac{V_o-\Delta V}{L}-\frac{R{x}_4}{L}-\frac{K_e{x}_5}{L}$$ $$(3)J_m\frac{d{\omega }_m}{dt}+B_s({\omega }_m-{\omega }_w)=K_{t}i$$ $$\dot{x_2}=\frac{K_t{x}_1}{J_m}-\frac{Bs{x}_2}{J_m}+\frac{Bs{x}_3}{J_m}$$ $$\dot{x_5}=\frac{K_t{x}_4}{J_m}-\frac{Bs{x}_5}{J_m}+\frac{Bs{x}_6}{J_m}$$ $$(4)J_w\frac{d{\omega }_W}{dt}-B_s({\omega }_m-{\omega }_w)=0$$ $$\dot{x_3}=\frac{B_s{x}_2}{J_w}-\frac{B_s{x}_3}{J_w}$$ $$\dot{x_6}=\frac{B_s{x}_5}{J_w}-\frac{B_s{x}_6}{J_w}$$ $$\begin{gathered} (5)F_L=\frac{2K_T}{R_W}{i}_L, \\ (6)F_R=\frac{2K_T}{R_W}{i}_R \end{gathered}$$ $$(7)\frac{dv}{dt}+K_{S}v-V_{T}r=K_V(F_L+F_R)\frac{v}{V_T}$$ $$(8)\frac{dr}{dt}+V_{T}r-K_{D}v=K_Y(F_L-F_R)R_M$$ $$\dot{x_7}=\frac{2K_v{K}_T{x}_7}{R_W{V}_T}{x}_4+\frac{2K_v{K}_T{x}_7}{R_W{V}_T}{x}_1-K_s{x}_7+V_T{x}_8$$ $$\dot{x_8}=\frac{2K_y{K}_T{R}_m}{R_W}{x}_1-\frac{2K_y{K}_T{R}_m}{R_W}{x}_4+K_D{x}_7-V_T{x}_8$$ $$(1)\Delta V=G_c\Delta \psi$$ $$\Delta V=G_c({\psi }_{ref}-\psi )$$

let $\psi =x_9$

$$\Delta V=G_c({\psi }_{ref}-x_9)$$ $$\therefore \dot{x_1}=\frac{V_o}{L}+\frac{G_C{\psi }_{ref}}{L}-\frac{G_C{x}_9}{L}-\frac{R{x}_1}{L}-\frac{K_e{x}_2}{L}$$ $$\dot{x_4}=\frac{V_o}{L}-\frac{G_c{\psi }_{ref}}{L}+\frac{G_c{x}_9}{L}-\frac{R{x}_4}{L}-\frac{K_e{x}_5}{L}$$ $$\dot{x_4}=\frac{V_o}{L}-\frac{Gc{\psi }_{ref}}{L}+\frac{G_c{x}_9}{L}$$ $$\dot{x_9}=x_8$$ $$\left[\begin{array}{c}\dot{x_1}\\ \dot{x_2}\\ \dot{x_3}\\ \dot{x_4}\\ \dot{x_5}\\ \dot{x_6}\\ \dot{x_7}\\ \dot{x_8}\\ \dot{x_9}\end{array}\right]=\left[\begin{array}{ccccccccc}-\frac{R}{L}& -\frac{K_e}{L}& 0& 0& 0& 0& 0& 0& \frac{-G_C}{L}\\ \frac{K_t}{J_m}& -\frac{B_s}{J_m}& \frac{B_s}{J_m}& 0& 0& 0& 0& 0& 0\\ 0& \frac{B_s}{J_w}& -\frac{B_s}{J_w}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& -\frac{R}{L}& -\frac{K_e}{L}& 0& \frac{2K_v{K}_T}{R_W{V}_T}& 0& \frac{G_C}{L}\\ 0& 0& 0& \frac{K_t}{J_m}& -\frac{B_s}{J_m}& \frac{B_s}{J_m}& 0& 0& 0\\ 0& 0& 0& 0& \frac{B_s}{J_w}& -\frac{B_s}{J_w}& 0& 0& 0\\ \frac{2K_v{K}_T}{R_W{V}_T}& 0& 0& \frac{2K_v{K}_T}{R_W{V}_T}& 0& 0& -K_s& V_T& 0\\ \frac{2K_y{K}_T{R}_m}{R_W}& 0& 0& -\frac{2K_y{K}_T{R}_m}{R_W}& 0& 0& K_D& -V_T& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ x_8\\ x_9\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L}& \frac{G_C}{L}\\ 0& 0\\ 0& 0\\ \frac{1}{L}& -\frac{G_C}{L}\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}{V}_o\\ {\psi }_{ref}\end{array}\right]$$

State Space:

• $\dot{x_1}=\frac{V_o}{L}+\frac{G_C{\psi }_{ref}}{L}-\frac{G_C{x}_9}{L}-\frac{R{x}_1}{L}-\frac{K_e{x}_2}{L}$
• $\dot{x_2}=\frac{K_t{x}_1}{J_m}-\frac{Bs{x}_2}{J_m}+\frac{Bs{x}_3}{J_m}$
• $\dot{x_3}=\frac{B_s{x}_2}{J_w}-\frac{B_s{x}_3}{J_w}$
• $\dot{x_4}=\frac{V_o}{L}-\frac{G_c{\psi }_{ref}}{L}+\frac{G_c{x}_9}{L}-\frac{R{x}_4}{L}-\frac{K_e{x}_5}{L}$
• $\dot{x_5}=\frac{K_t{x}_4}{J_m}-\frac{Bs{x}_5}{J_m}+\frac{Bs{x}_6}{J_m}$
• $\dot{x_6}=\frac{B_s{x}_5}{J_w}-\frac{B_s{x}_6}{J_w}$
• $\dot{x_7}=\frac{2K_v{K}_T{x}_7}{R_W{V}_T}{x}_4+\frac{2K_v{K}_T{x}_7}{R_W{V}_T}{x}_1-K_s{x}_7+V_T{x}_8$
• $\dot{x_8}=\frac{2K_y{K}_T{R}_m}{R_W}{x}_1-\frac{2K_y{K}_T{R}_m}{R_W}{x}_4+K_D{x}_7-V_T{x}_8$
• $\dot{x_9}=x_8$

function xdot = rover(x,u);
 
global Vo;
 
global Gc;
 
global Bs;
 
global Kt;
 
global Ke;
 
global Ky;
 
global Jw;
 
global Jm;
 
global Rm;
 
global L;
 
global Pr;
 
xdot(1,1) = (Vo+Gc*Pr-Gc*x(9)-R*x(1)-Ke*x(2) ) /L;
 
xdot(2,1) = (Kt*x(1)-Bs*x(2)+Bs*x(3))/Jm;
 
xdot(3,1) = (Bs*x(2)-Bs*x(3))/Jw;
 
xdot(4,1) = (Vo - Gc*Pr + Gc*x(9)-R*x(4)-Ke*x(5))/L;
 
xdot(5,1) = (Kt*x(4) - Bs*x(5) + Bs*x(6))/Jm;
 
xdot(6,1) = (Bs*x(5)-Bs*x(6))/Jw;
 
xdot(7,1) = (2*Kt*Kv*x(7)*x(4))/(Rw*Vt) + (2*Kt*Kv*x(7)*x(1))/(Rw*Vt) - Ks*x(7) + Vt*x(8);
 
xdot(8,1) = (2*Ky*Kt*Rm*x(1))/Rw - (2*Ky*Kt*Rm*x(4))/Rw + Kd*x(7) - Vt*x(8);
 
xdot(9,1) = x(8);

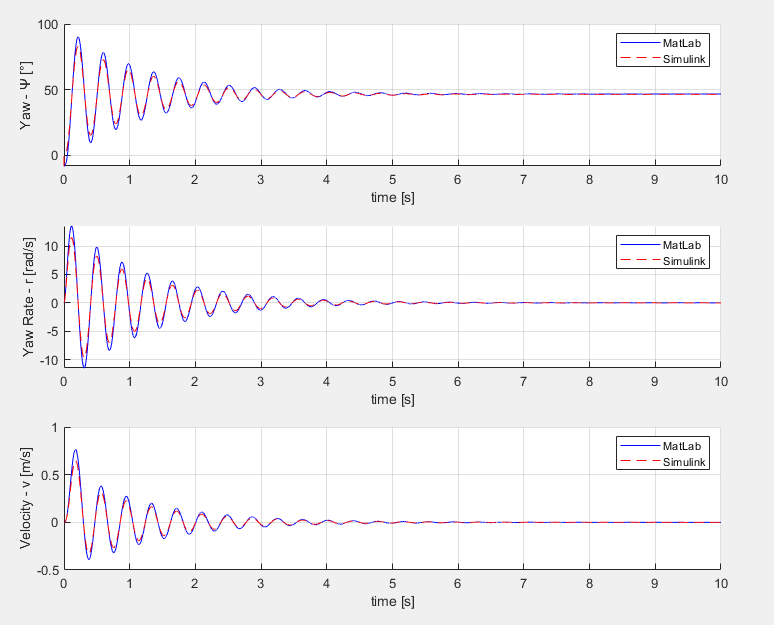
legend('MatLab', 'Simulink')