DSP Things To Memorise

Formulas

Euler

$e^{j\alpha }+e^{-j\alpha }=2\cos (\alpha )$ $e^{j\alpha }-e^{-j\alpha }=2j\sin (a)$

IIR Formulas

$s=\frac{2}{T}\frac{z-1}{z+1}$ ${\Omega }_c=\frac{2}{T}\tan \frac{{\omega }_c}{2}$

Code

DFT Python

N = len(signal)
X = np.zeros(N)
for k in range(N):
	for n in range(N):
		X[k] += signal[n] * np.exp(-2j * np.pi * k * (n/N))

IDFT

N = len(signal)
x = np.zeros(N)
for n in range(N):
	for k in range(N):
		x[n] += X[k] * np.exp(2j * np.pi * k * (n/N))
x /= N

Getting a WAV file (assuming 16bit):

input_wav = wavfile.get("file.wav")
signal = input_wav / (2**15)

Making a WAV file (assuming 16 bit):

signal = ...
output_wav = signal * (2**15)

Plotting DB Frequency Pseudocode:

# assuming f_sig is already the dft of a signal
f_sig = X[:N//2] # take only first half of frequency response
f_db = 20 * np.log10( np.abs(f_sig) )
freq_axis = [idx * f_s / N for idx in range(N//2)]
plot(y=f_db,x=freq_axis)

Slicing and Filters:

"""
Your cutoff frequency can be translated into a sample number using
cutoff = int(f_c / f_s * N)
"""
f_s = 10000
N = len(signal)
f_low = 1000
f_high = 3000
 
cutoff_low = int(f_low / f_s * N)
cutoff_high = int(f_high / f_s * N)
 
# Highpass
signal[:cutoff_low] = 0  # Up until cutoff = 0
signal[-cutoff_low:] = 0 # Inverse of line above, just the aliased version
 
# 0 1 2 3 4 5 6 7 8 9 X   <- Initial
#     2 3 4 5 6 7 8 9 X   <- Line 1
#     2 3 4 5 6 7 8       <- Line 2
 
 
# Lowpass
signal[cutoff_high:N//2] = 0
signal[N//2:-cutoff_high] = 0
 
# 0 1 2 3 4 5 6 7 8 9 X <- Initial
# 0 1 2     5 6 7 8 9 X <- Line 1
# 0 1 2           8 9 X <- Line 2
 
# Bandstop
signal[cutoff_low:cutoff_high] = 0
signal[-cutoff_high:-cutoff_low] = 0
 
# 0 1 2 3 4 5 6 7 8 9 X <- Initial
# 0       4 5 6 7 8 9 X <- Line 1
# 0       4 5 6       X <- Line 2
 
# Bandpass is just highpass + lowpass
 
# With bounds around target
bound = 50
cutoff_bound = int(bound / f_s * N)
 
# Lowpass Ex:
signal[:cutoff_low+bound] = 0
signal[-cutoff_low-bound:] =0
 

FIR Knowledge

$$\text{Number of Taps: }\frac{f_s}{f_c\text{ or }BW}$$

Where you use either the cutoff frequency, or the bandwidth of the filter

FIRs don’t necessarily perform convolutions as there is a finite range as opposed to the $-\infty \to \infty$ range of convolutions

Calculate frequency response: Sub in $e^{j\omega }$ for $z$ Example:

$$\begin{array}{rl}H(z)& =\frac{1}{1+0.5z^{-1}}\\ H(e^{j\omega })& =\frac{1}{1+0.5e^{-j\omega }}=\frac{1}{1-0.5\cos \omega +0.5j\sin \omega }\\ |H(e^{j\omega })|& =\frac{1}{\sqrt{(1-0.5\cos \omega {)}^2-(0.5\sin \omega {)}^2}}\\ \text{At DC: }\omega =0,|H(e^{j\omega })|& =\frac{1}{\sqrt{(0.5{)}^2}}=2\\ \text{At Nyquist: }\omega =\pi ,& =\frac{1}{\sqrt{1.5^2-0^2}}\approx 0.67\end{array}$$

IIR Knowledge

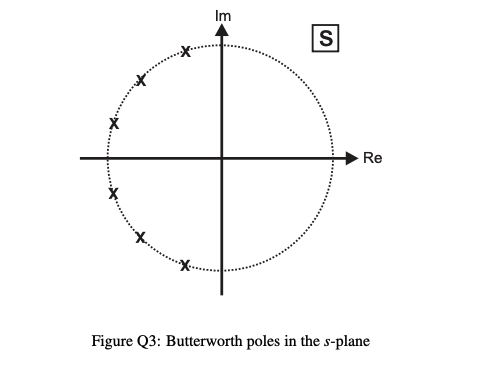Poles on S-Plane Right to Left, in groups of 2, to form a chain of second order filters

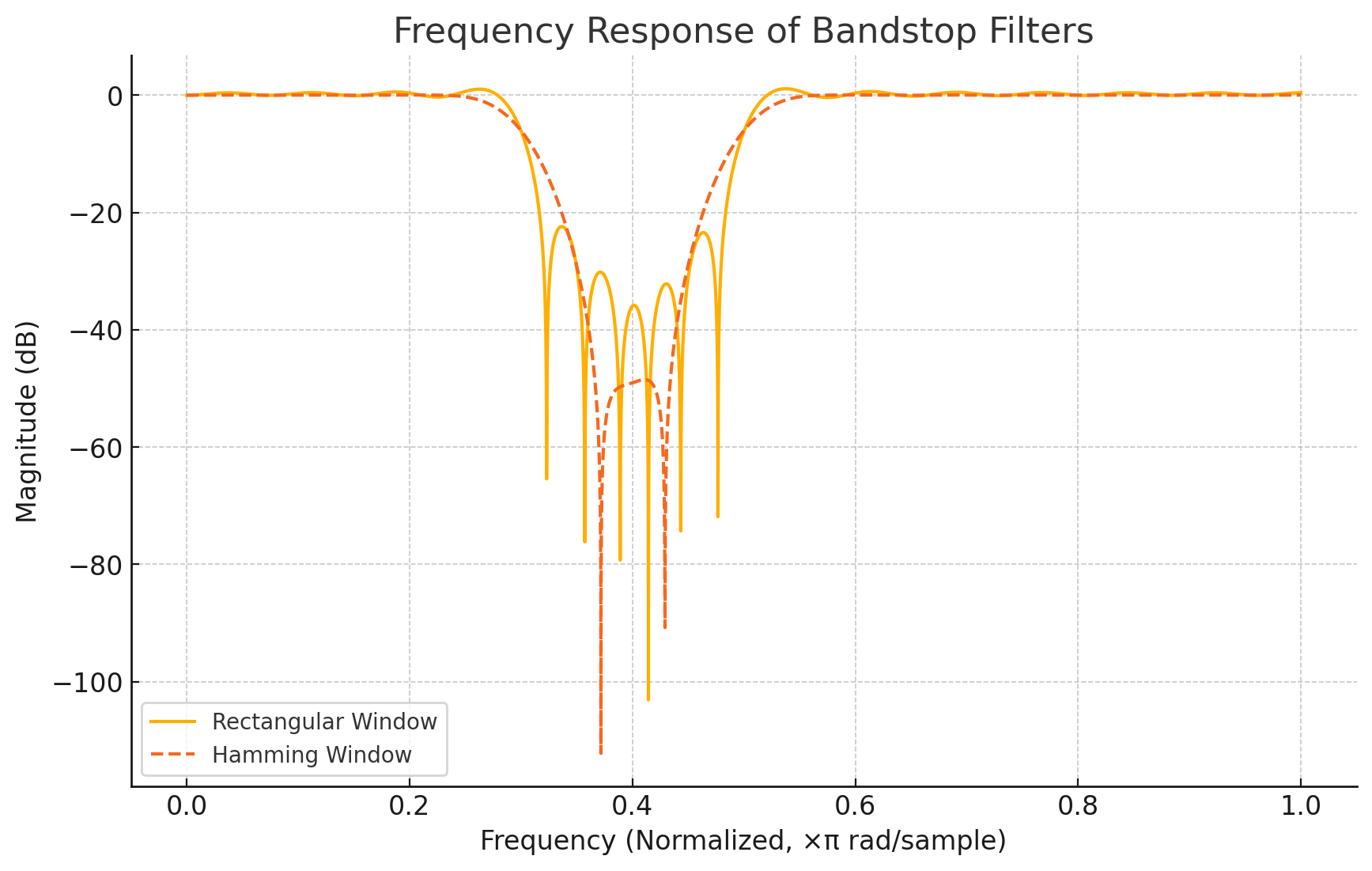
Higher Damping on Window is Wider Transition from stop to passband. Blackman highest, Hamming better for lower damping

When asked on a transfer like this:

$H(z)=\frac{1-2\cos ({\omega }_0)z^{-1}+z^{-2}}{1-2r\cos ({\omega }_0)z^{-1}+r^2{z}^{-2}}$

In this example, r affects the stability and notch width and attenuation depth. ${\omega }_0$ affects the centre frequency of the notch, and therefore the cutoffs too

DATAFLOW: $H(z)=\frac{(1-e^{j{\omega }_0}{z}^{-1})(1-e^{-j{\omega }_0}{z}^{-1})}{(1-r{e}^{j{\omega }_0}{z}^{-1})(1-r{e}^{-j{\omega }_0}{z}^{-1})}$

$$\begin{array}{rl}\text{Numerator: }& 1-(e^{j{\omega }_0}+e^{-j{\omega }_0})z^{-1}+z^{-2}=1-2\cos ({\omega }_0)z^{-1}+z^{-2}\\ \text{Denominator: }& 1-r(e^{j{\omega }_0}+e^{-j{\omega }_0})z^{-1}+r^2{z}^{-2}=1-2r\cos ({\omega }_0)+r^2{z}^{-2}\end{array}$$