FIR Linear Phase Filter

Beyond portability and ease of set up, there are in fact FIR filters that can even operate better than their analog versions. Linear phase in this context means that the group delay (${\tau }_g$) is constant, i.e. all frequencies are delayed by the exact same time

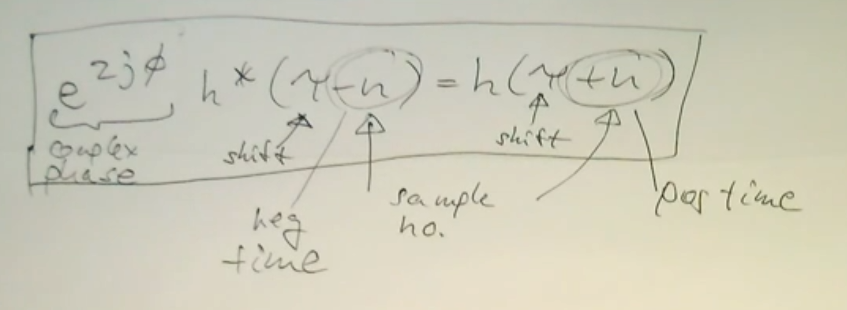
How do we construct this? We know our constraint is that: $\tau (\omega )=const$ $\tau (\omega )=-\frac{d\theta (\omega )}{d\omega }$ where $\text{arg}H(e^{j\omega })$ → $d\theta (\omega )$ , and denotes the phase angle of the frequency response $H(e^{j\omega })$ So we need a constant $H(e^{j\omega })$ with constant group delay, and then just inverse fourier it

$$\begin{array}{c}H\left(e^{j\omega }\right)=\underset{\text{real }}{\underbrace{B(\omega )}}\underset{\text{complex phase }}{\underbrace{e^{-j\omega \tau +j\varphi }}}\\ \arg H\left(e^{j\omega )}=-\omega \tau +\varphi =\theta (\omega )\right).\\ -\frac{d\theta (\omega )}{d\omega }=-\tau \begin{array}{c}\text{ constant }\\ \text{ group delay! }\end{array}\end{array}$$ $$\begin{array}{rl}h(n)& =\frac{1}{2\pi }{\int }_{-\pi }^{\pi }H(e^{j\omega })e^{j\omega }d\omega \\ & =\frac{1}{2\pi }{\int }_{-\pi }^{\pi }B(\omega )e^{-j\omega \tau \underset{\text{phase}}{\underbrace{+j\varphi }}}{e}^{j\omega n}d\omega \\ & =\frac{1}{2\pi }{e}^{j\varphi }{\int }_{-\pi }^{\pi }B(\omega )e^{-j\omega (\tau -n)}d\omega \\ & =\frac{1}{2\pi }{e}^{j\varphi }{\int }_{-\pi }^{\pi }B(\omega )e^{j\omega (n-\tau )}d\omega \\ h(n+\tau )& =\frac{e^{j\varphi }}{2\pi }\underset{\text{b(n), inverse FT of B(}\omega )}{\underbrace{{\int }_{-\pi }^{\pi }B(\omega )e^{j\omega n}d\omega }}\\ & =\frac{e^{j\varphi }}{2\pi }b(n)\\ b(n)& =h(n+\tau )2\pi e^{-j\varphi }\\ b^{\ast }(-n)& =b(n)\\ & \\ & \text{I’m lost, 23:10, 005 FIR Filters}\end{array}$$

????

Because $e^{2j\varphi }$ creates a unit circle, and we need both $h^{\ast }$ and $h$ to be real, we know the only two valid values are going to be $\pm 1$ for the $e^{2j\varphi }$ term

So we can simplify to:

$$\pm h^{\ast }(\tau -n)=h(\tau +n)$$

And we can think of this graphically as $\tau$ is the right shift from the origin, and that this is valid for any symmetric/antisymmetric (even/odd) function

i.e. we have linear phase for any symmetrical or antisymmetric impulse response

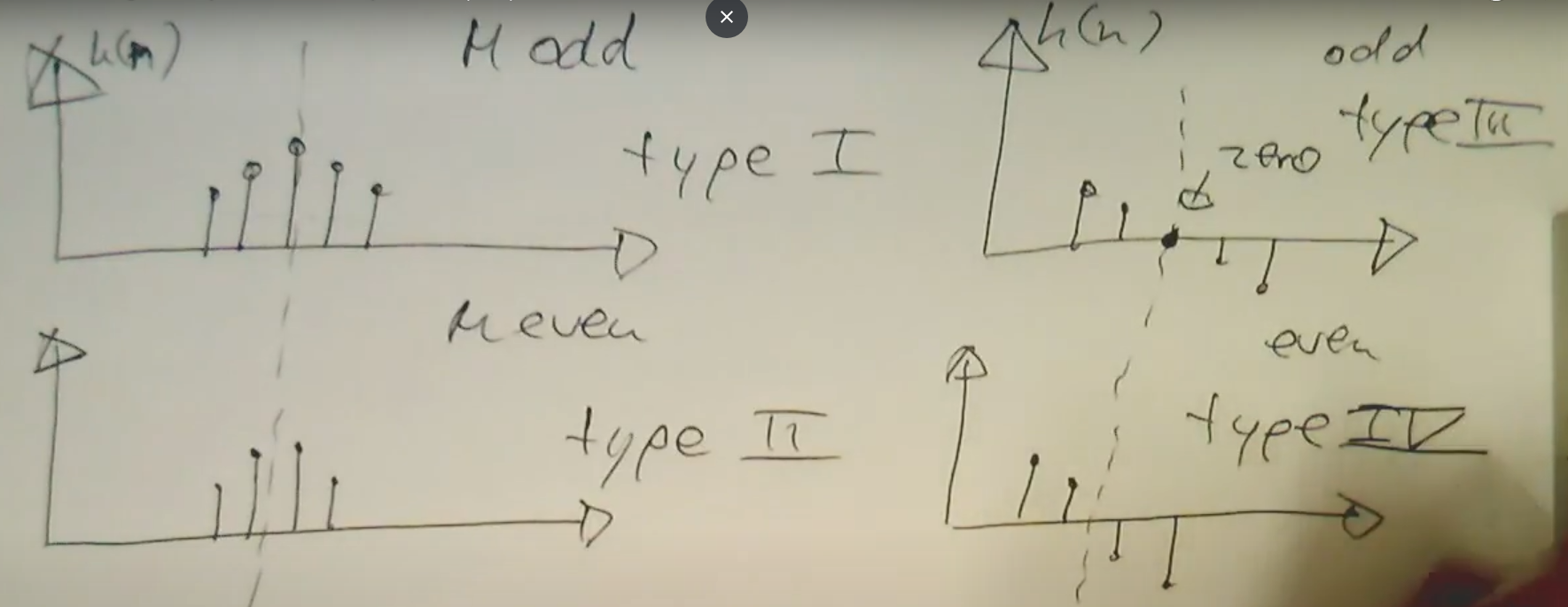
Implementation

If $M$ is our number of taps, then $\tau$ is usually $\frac{M}{2}$

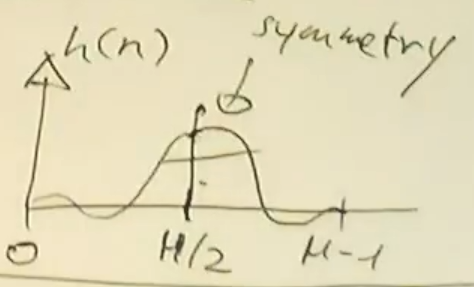
We sort of waste half our taps to make it linear phase

4 Types in practice: