Bode Diagram

Bode diagrams or Bode plots are an alternative method for displaying frequency responses graphically. Instead of plotting the phase and gain information on the same plot (as in the polar locus) the Bode plot uses two separate plots, one for the magnitude (or gain) and the other for the phase.

Polar loci are (for complex systems) hard to draw accurately without reasonable computations. Bode plots are often used instead since it is fairly easy to obtain accurate sketches. The plots are of:

• Gain (measured in $\text{dB}=20\log 10|G(j\omega )|$)
• Phase, $\arg G(j\omega )$ (usually in degrees), Plotted against frequency, $\omega$, in usually in rad/s on a logarithmic scale.

Thus by using these conventions, in both the magnitude and phase plots we can break down the overall magnitude or phase into a sum of individual components. We therefore only need to consider the elementary diagrams for simple components which can then be combined for more complex systems.

Strategy:

Rewrite TF into Correct Form

We would like to rewrite this so the lowest order term in the numerator and denominator are both unity. This is best done through examples: i)

$$30\ast \frac{10}{50}\ast \frac{(1+s/10)}{s^2/50+3s/50+1}=6\frac{1+\frac{s}{10}}{\frac{s^2}{50}+\frac{3s}{50}+1}$$

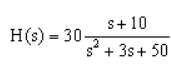
Lowest order here is 0, equal to 1

ii)

$$30\ast \frac{5}{50}\ast \frac{\frac{s}{1}}{s^2/50+3s/50+1}=3\frac{\frac{s}{1}}{\frac{s^2}{50}+\frac{3s}{50}+1}$$

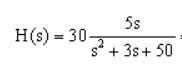
The lowest power in the numerator was 1, therefore we solved as such

iii) 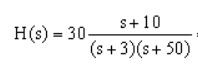In this example the denominator was already factored.  In cases like this, each factored term needs to have unity as the lowest order power of s (zero in this case).

$$30\ast \frac{10}{3\ast 50}\ast \frac{(\frac{s}{10}+1)}{(\frac{s}{3}+1)(\frac{s}{50}+1)}=2\frac{(\frac{s}{10}+1)}{(\frac{s}{3}+1)(\frac{s}{50}+1)}$$

Separate the TF into parts

There are 7 types of parts

1. A constant
2. Poles at the origin
3. Zeros at the origin
4. Real Poles
5. Real Zeros
6. Complex conjugate poles
7. Complex conjugate zeros

Look at ex i) : $6\frac{1+\frac{s}{10}}{\frac{s^2}{50}+\frac{3s}{50}+1}$ - Constant of 6 - Zero at Complex Conj Poles at roots of $s^2+3s+50$ ($s=-1.5\pm j6.9$) It is better instead to look at our standard form $s^2+2\xi {\omega }_{n}s+{\omega }_n^2$ , which means ${\omega }_n^2=50\to {\omega }_n=7.07$, $\xi {\omega }_n=1.5\to \xi =0.21$

ex ii): $3\frac{\frac{s}{1}}{\frac{s^2}{50}+\frac{3s}{50}+1}$ Constant of 3 Zero at origin ${\omega }_n^2=50\to {\omega }_n=7.07$, $\xi {\omega }_n=1.5\to \xi =0.21$
ex iii): $2\frac{(\frac{s}{10}+1)}{(\frac{s}{3}+1)(\frac{s}{50}+1)}$ Constant of 2 Zero at $s=-10$ Poles at $s=-3,s=-50$

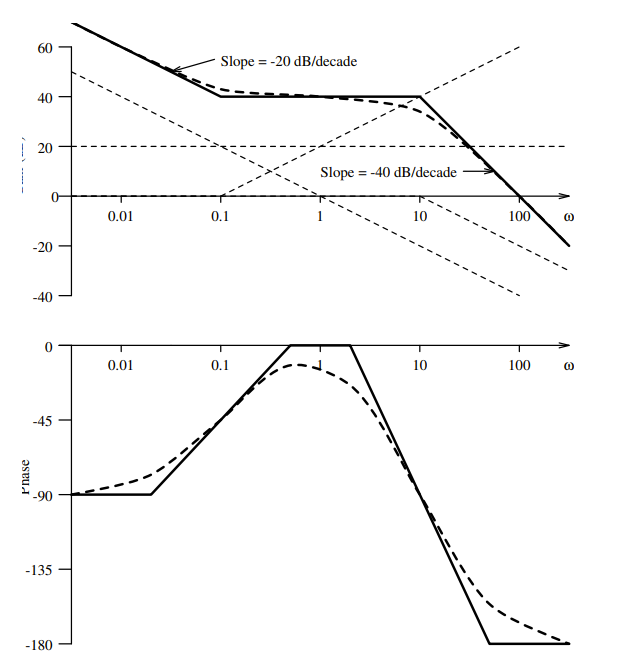
Draw the Bode diagram for each part.

Term	Magnitude	Phase
Constant: K	$20log10(\Vert K\Vert )$	$K>0:0^o\Vert K<0:\pm 180^o$
Pole at Origin (Integrator) $\frac{1}{s}$	-20 dB/decade passing through 0 dB at $\omega =1$	$-90^o$
Zero at Origin (Differentiator) $s$	+20 dB/decade passing through 0 dB at ω=1_ (Mirror image, around x axis,of Integrator)_	$+90^o$
Real Pole $\frac{1}{\frac{s}{{\omega }_0}+1}$	1. Draw low frequency asymptote at 0 dB. 2. Draw high frequency asymptote at -20 dB/decade. 3. Connect lines at ω0.	1. Draw low frequency asymptote at 0° 2. Draw high frequency asymptote at -90° 3. Connect with a straight line from $0.1\cdot {\omega }_0$ to $10\cdot {\omega }_0$
Real Zero $\frac{s}{{\omega }_0}+1$	1. Draw low frequency asymptote at 0 dB. 2. Draw high frequency asymptote at +20 dB/decade. 3. Connect lines at ω0. (Mirror image, around x-axis, of Real Pole)	1. Draw low frequency asymptote at 0° 2. Draw high frequency asymptote at +90° 3. Connect with a straight line from $0.1\cdot {\omega }_0$ to $10\cdot {\omega }_0$ (Mirror image, around x-axis, of Real Pole about 0°)
Underdamped Poles (Complex conjugate poles) $\frac{1}{(\frac{s}{{\omega }_0}{)}^2+2\xi (\frac{s}{{\omega }_0})+1}$	1. Draw low frequency asymptote at 0 dB. 2. Draw high frequency asymptote at -40 dB/decade. 3. Connect lines at ω0. 4. If ζ<0.5, then draw peak at ω0 with amplitude     $\Vert H(j\omega 0)\Vert =-20\cdot {\log }_{10}(2\zeta )$, else don’t draw peak (it is very small).	1. Draw low frequency asymptote at 0° 2. Draw high frequency asymptote at -180° 3. Connect with straight line from $\omega =\frac{{\omega }_0}{10^{\xi }}$ to ${\omega }_0\ast 10^{\xi }$
Underdamped Zeros (Complex conjugate zeros) $(\frac{s}{{\omega }_0}{)}^2+2\xi (\frac{s}{{\omega }_0})+1$	1. Draw low frequency asymptote at 0 dB. 2. Draw high frequency asymptote at +40 dB/decade. 3. Connect lines at ω0. 4. If ζ<0.5, then draw peak at ω0 with amplitude      $\Vert H(j\omega 0)\Vert =+20\cdot lo{g}_{10}(2\zeta )$, else don’t draw peak (it is very small). (Mirror image, around x-axis, of Underdamped Pole)	1. Draw low frequency asymptote at 0° 2. Draw high frequency asymptote at -180° 3. Connect with straight line from $\omega =\frac{{\omega }_0}{10^{\xi }}$ to ${\omega }_0\ast 10^{\xi }$

Examples

Simple Gain

$G(s)=K$

$$\begin{array}{rl}20\log |G|& =20\log K\\ \arg G(j\omega )& =0^o\end{array}$$

An Integrator

$G(s)=\frac{1}{s},G(j\omega )=\frac{1}{j\omega }$

$$\begin{array}{rl}20\log |G|=-20\log \omega & =-20x\text{ if }x=\log \omega \\ \arg G(j\omega )& =-90^o\end{array}$$

Magnitude Plot: 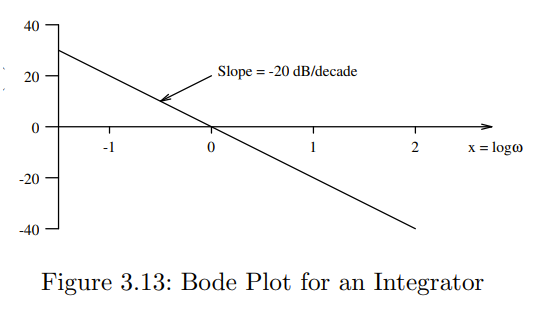Phase Plot is skipped, too simple

Simple Lag

$G(s)=\frac{1}{1+s/{\omega }_c}$,

$$\begin{array}{rl}20\log |G|& =-10\log (1+\frac{{\omega }^2}{{\omega }_c^2})\\ & \approx -10\log 1=0\omega \ll {\omega }_c\\ & =-10\log 2=-3\text{dB}\omega ={\omega }_c({\omega }_c\text{: corner frequency})\\ & \approx -20\log \frac{\omega }{{\omega }_c}\omega \gg {\omega }_c\\ & =20\log {\omega }_c-20x\\ & \text{ This is a straight line through 0dB when }\omega ={\omega }_c\end{array}$$

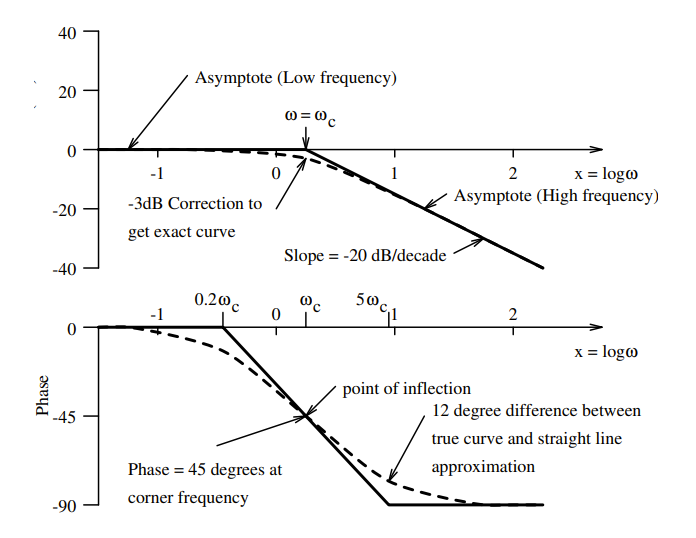It is also possible to make a straight line approximation of the phase as shown in the lower figure.

Simple Lead

$G(s)=1+s/{\omega }_c$,

$$\begin{array}{rl}20\log |G|& =10\log (1+\frac{{\omega }^2}{{\omega }_c^2})\\ & \approx 10\log 1=0\omega \ll {\omega }_c\\ & =10\log 2=3\text{dB}\omega ={\omega }_c({\omega }_c\text{: corner frequency})\\ & \approx 20\log \frac{\omega }{{\omega }_c}\omega \gg {\omega }_c\\ & =20x-20\log {\omega }_c\\ & \text{ This is a straight line through 0dB when }\omega ={\omega }_c\end{array}$$

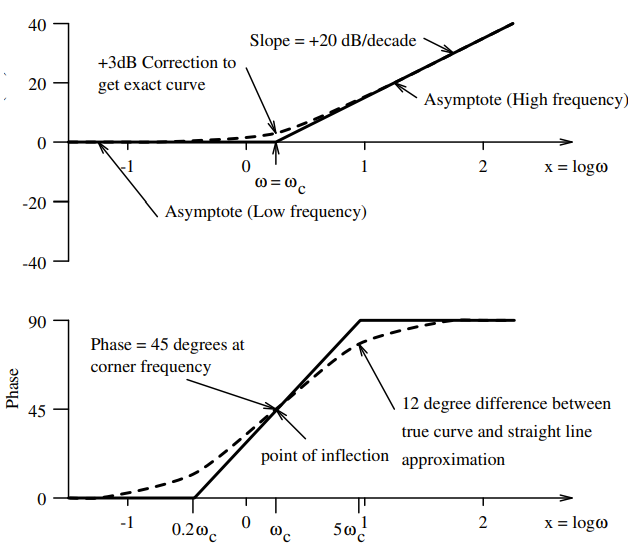
Gain and Phase Margin:

You can create the Gain and Phase Margin for our Bode Diagram using the following rules:

Gain Margin

The magnitude difference to $0$dB at the frequency at which the phase reaches $-180^o$ .

Phase Margin

$\varphi$ is equal to the phase difference from $-180^o$ at the frequency at which the magnitude is $0$dB.

Ex ($G_o(s)=\frac{1}{s(s+1)(s+2)}$):

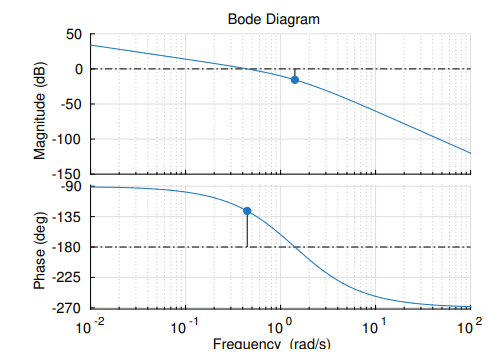
Worked Ex:

Ex 1:

Original: Point 3.3.2 Page 28 Part 2

$$G(s)=\frac{10(1+10s)}{s(1+s/10{)}^2}$$

We can split this into mutiple sections:

• $10$ - The Gain Term
• $(1+10s)$ - The Lead Term
• $\frac{1}{s}$ - The Integrator Term
• $(1+s/10)$ - The two lag terms

From this we can plot all of these on our two plots as straight line approximations:

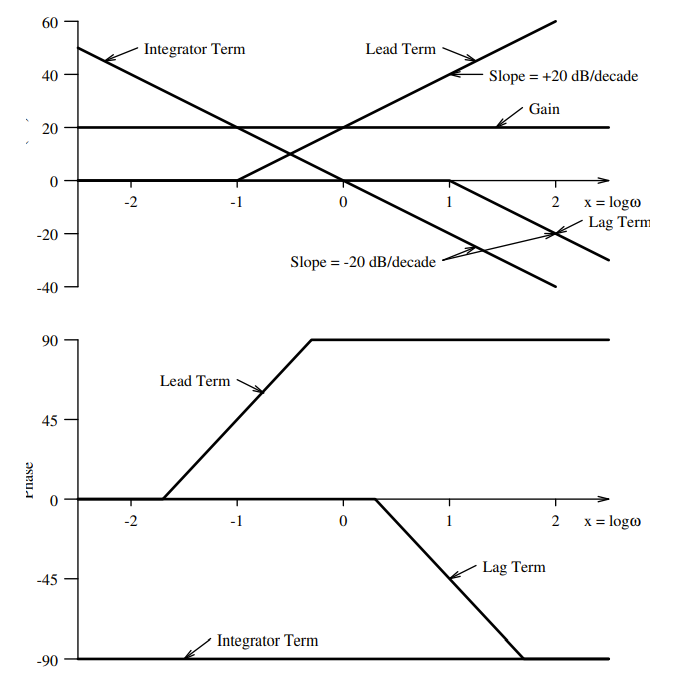Note: from here, we are converting from using $x=\log \omega$ to using $\omega$ This is fine, as we will logartihmically space our new graph.

Magnitude Plot

$$\begin{array}{cl}0<\omega <0.1& \text{ Slope }=-20\mathrm{dB}/\text{ decade }\\ \omega =0.1& +3\mathrm{dB}\text{ Correction }\\ 0.1<\omega <10& \text{ Slope }=0\mathrm{dB}/\text{ decade }\\ \omega =10& -6\mathrm{dB}\text{ Correction }\\ 10<\omega <\infty & \text{ Slope }=-40\mathrm{dB}/\text{ decade }\end{array}$$

Phase Plot

$$\begin{array}{cl}0<\omega <0.02& \text{ Angle }=-90^{\circ }\\ \omega =0.1& \text{ Angle }=-45^{\circ }\\ 0.5<\omega <2& \text{ Angle }=0^{\circ }\\ \omega =10& \text{ Angle }=-90^{\circ }\\ 50<\omega <\infty & \text{ Angle }=-180^{\circ }\end{array}$$

Which leads us to: