Control 3

Course

Control Lab 1 Notes

Root Locus

First Order Systems Second Order Systems Transfer Function Types of Input Signal Block Diagrams Poles and Zeros of a Dynamic System Routh’s Stability Criterion Frequency Domain Analysis Nyquist Stability Theorem Point of Instability Analysis Bode Diagram Laplace Transform

Data Sheet

Standard System Responses

First Order Systems

A standard first order system has a differential equation:

$$\frac{dy}{dt}+ay=ku$$

This has a Laplace Transform Representation:

$$Y(s)=\frac{k}{s+a}U(s)$$

The step response of this system, assuming zero initial conditions is:

$$y(t)=k\left(1-e^{-at}\right)$$

The time constant is defined as $\tau =\frac{1}{a}$ and the final output of the system is $k$. The value of $y(t)$ is defined in terms of $\tau$ by the following table.

Time	$\tau$	$2\tau$	$3\tau$	$4\tau$	$5\tau$
Output	$0.6321k$	$0.8647k$	$0.9502k$	$0.9817k$	$0.9933k$

Second Order Systems

A standard second order system has a differential equation:

$$\frac{d^{2}y}{d{t}^2}+2\zeta {\omega }_n\frac{dy}{dt}+{\omega }_n^{2}y=k{\omega }_n^{2}u$$

This has a Laplace Transform Representation:

$$Y(s)=\frac{k{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}U(s)$$

The step response of this system, assuming zero initial conditions is:

$$y(t)=k\left[1-e^{-\zeta {\omega }_{s}t}\left(\cos \omega t+\frac{\zeta {\omega }_n}{\omega }\sin \omega t\right)\right]$$

Where $\omega ={\omega }_n\sqrt{1-{\zeta }^2}$ and the final output of the system is $k$. The relationship between the angular position of the poles, $\theta$, damping factor, $\zeta$, and the percentage overshoot, $h=e^{\frac{{ϵ}_{\omega }\pi }{\omega }}=e^{-\pi \cos \theta }$, which occurs at time $t=\frac{\pi }{\omega }$ is shown by the following table.

$\theta$	$0$	$30^{\circ }$	$45^{\circ }$	$60^{\circ }$	$75^{\circ }$	$90^{\circ }$
Damping Factor	$1.0$	$0.866$	$0.707$	$0.5$	$0.26$	$0.0$
Percentage Overshoot	$0.0\%$	$0.4\%$	$4.3\%$	$16.3\%$	$43.9\%$	$100\%$

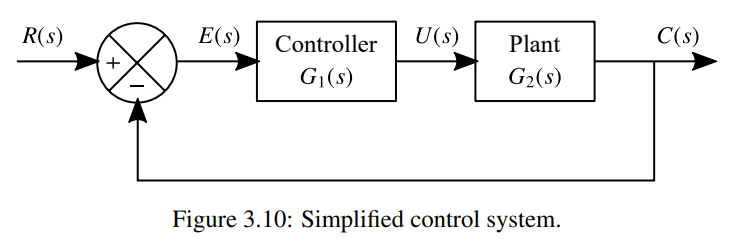
Block Diagrams

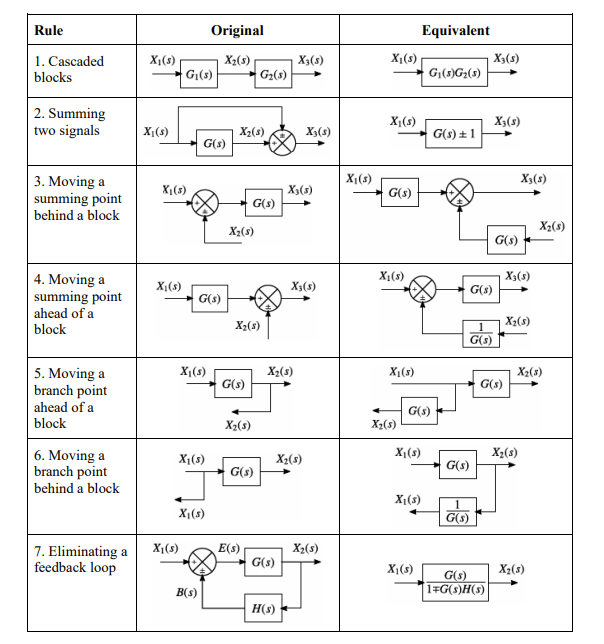
Characteristics of the Response of an Underdamped Second-Order System to a Step Input

The response of a second-order system to a step input can be characterised by four properties:

$$\begin{array}{rl}\text{Rise Time: }& t_r=\frac{1}{{\omega }_d}\left[\pi -{\tan }^{-1}\left(\frac{\sqrt{1-{\zeta }^2}}{\zeta }\right)\right]\\ \text{Peak Time: }& t_p=\frac{\pi }{{\omega }_d}\\ \text{Max Overshoot: }& M_p=x(\infty )e^{-\frac{\pi \zeta }{\sqrt{1-{\zeta }^2}}}\text{ or }{M}_p=100e^{-\zeta {\omega }_n{t}_p}\%\\ \text{Settling Time: }& t_s=\frac{3}{\zeta {\omega }_n}\end{array}$$

Where:

• ${\omega }_n$ is the undamped natural frequency of the system,
• $\zeta$ is the damping ratio,
• $x(\infty )=$ $x_{ss}$ is the steady-state value
• ${\omega }_d$ is the damped natural frequency, given by ${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}$

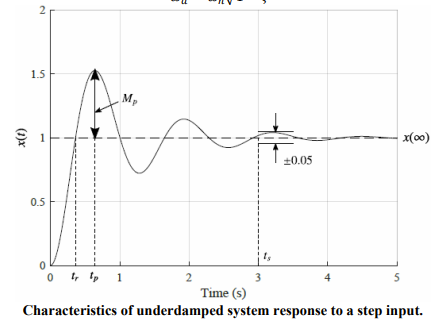
Basic Controller Set Up

Error Transfer Function

$$\frac{E(s)}{R(s)}=\frac{1}{1+G_1(s)G_2(s)}$$

Where:

Transfer Function

Control 3 Worked Example Portal