Root Locus

Abstract

The Root Locus diagram/analysis is a graphical method for examining how the roots of a system change under the shifting of a variable from $0\to \infty$ , typically the gain of a section of the controller.

The so-called Calibration Equation and the Angle Criterion can be used to work out possible locations of the closed-loop poles (i.e. the root locus) as K varies.

It also follows from our Angle Criterion that any point can be on the real axis of the root locus, if and only if there is an odd number of singularities (roots and zeros), to their right.

Always from form:

$$1+KG(s)=0orA(s)+KB(s)=0$$

Or alternatively:

$$1+K\frac{Q(s)}{P(s)}$$

Procedure for drawing the root locus

The complete procedure for drawing the root locus is as follows:

1. Identify number of poles ($n$), zeros ($m$), and determine the relative order ($n-m$).
2. Plot the location of the poles (x) and zeros (o) in the complex plane (on graph paper).
3. Determine which parts of the real axis are on the locus (Rule 5 Odd critical frequencies).
4. Identify the number and directions of the asymptotes (Angle of Asymptotes)
5. Determine where the asymptotes meet (Centroid of Asymptotes) and draw the asymptotes on the graph.
6. Identify any poles uniquely connected to zeros along the x-axis — these form one branch of the locus.
7. If two poles on the axis need to become complex to go to asymptotes, they must pass through a double point found by the solutions of $\frac{d{G}_o}{dS}=0$ (Double Points).
8. Optional: If there are complex poles or zeros the angles of arrival or departure need to be determined.

10 Rules Of Drawing

Rule 1: n loci

There are n lines (loci), where n is the degree of $G(s)$ (or the greater of $Q(s)||P(s)$.

Rule 2: Movement of roots due to K

As $k$ increases from $0$ to $\infty$, the roots of the system move from the poles of $G(s)$ to the zeros of $G(s)$

i.e.

$$1+K\frac{Q(s)}{P(s)}=0=P(s)+KQ(s)$$

Therefore: Poles of $G(s)$ when $P(s)=0$ Zeros of $G(s)$ when $Q(s)=0$

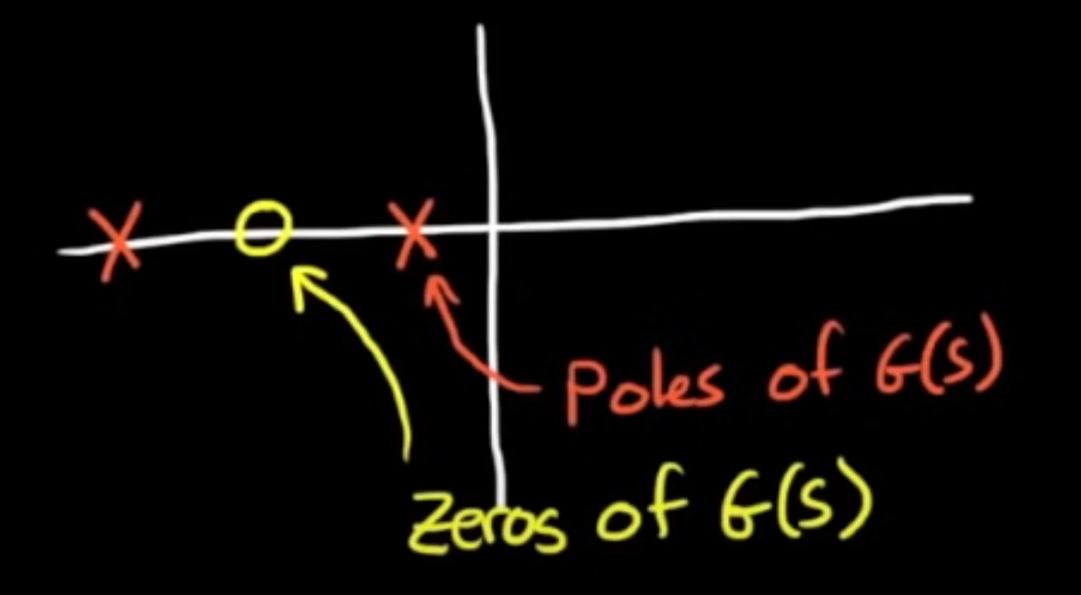
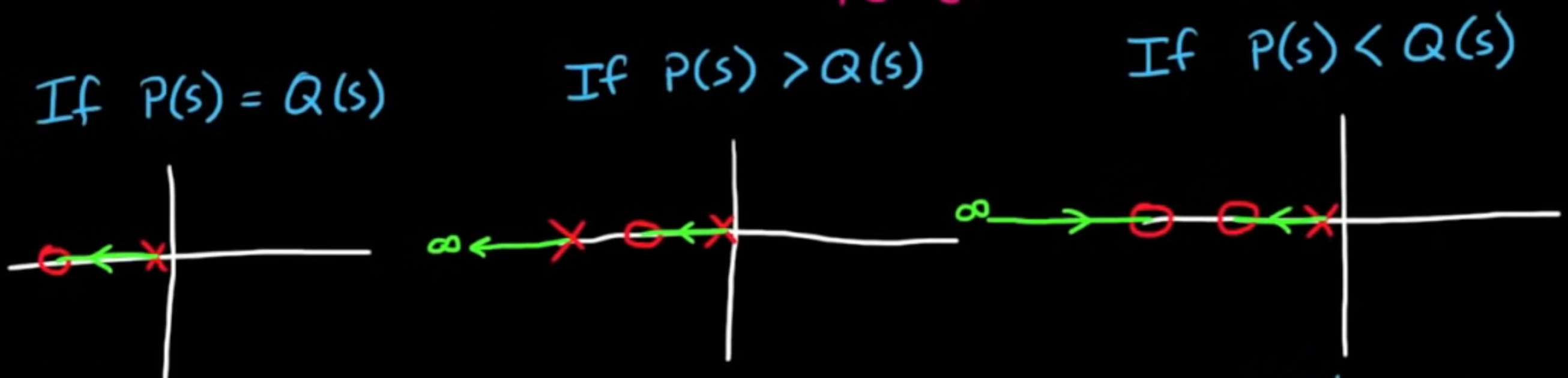
i.e. closed loop poles travel from open loop poles of $G(s)$ to zeros of $G(s)$ if poles and zeros are unbalanced, they “pair” with $\pm \infty$

Rule 3: Complex roots always have pairs

You can never get a complex root without its complex conjugate pair

Rule 4: A root will never cross its own path:

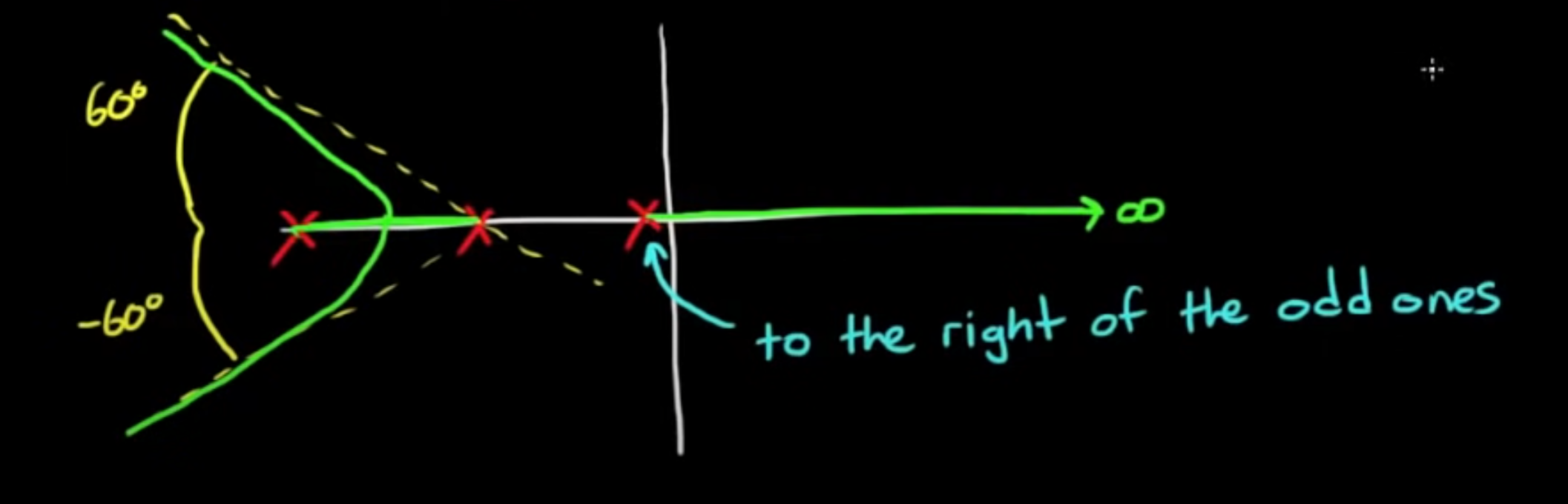
Rule 5: Odd critical frequencies

The portion of the real axis to the left of an odd number of open loop poles and zeros are part of the loci

Rule 6: Breakout/in

Lines leave the real axis (breakout) and enter (breakin) at $90^o$

Rule 7: Circles:

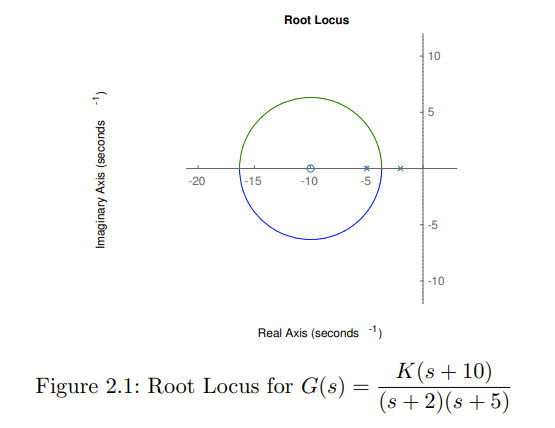
Consider the case that the real axis (from left to right) is zero, pole, pole. It follows that one of the poles must coincide with the zero, however the poles block each other. In this case, the vectors approach each other, much in a similar way as to when there is no zero, and then they perfectly encircle the zero before rejoining the real axis, and splitting off, one towards infinity and the other towards the zero.

Rule 8: Lines go to infinity along asymptotes.

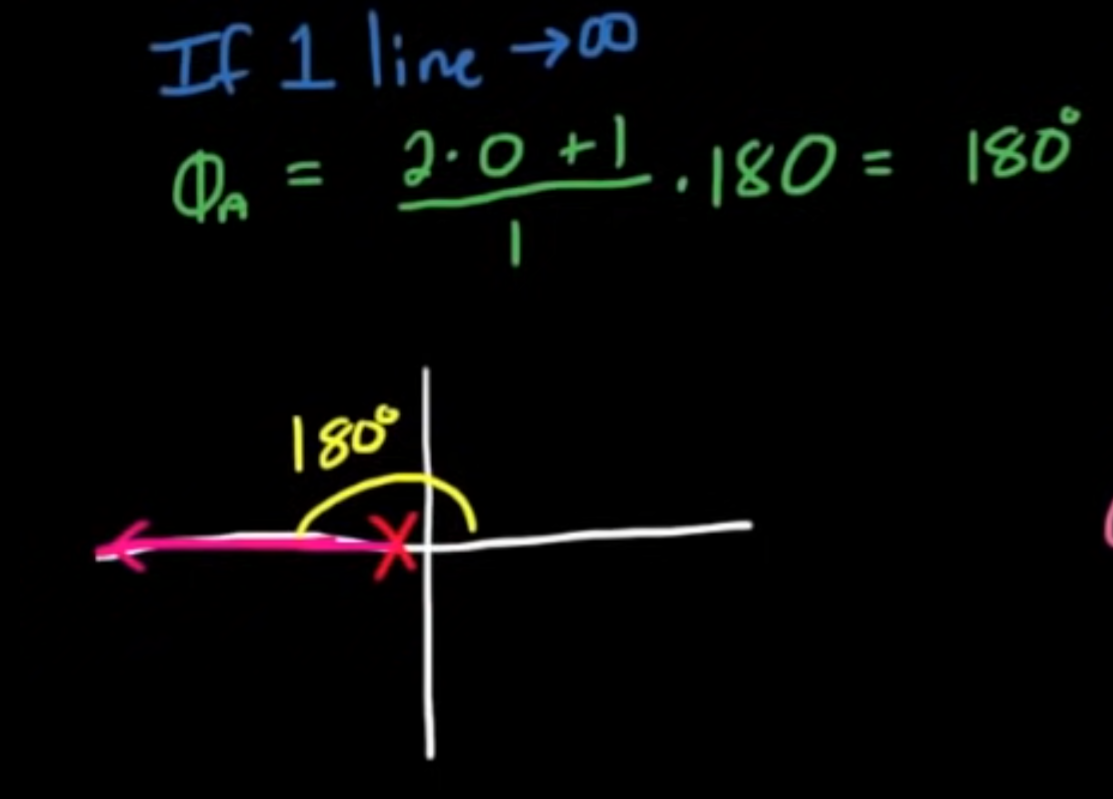
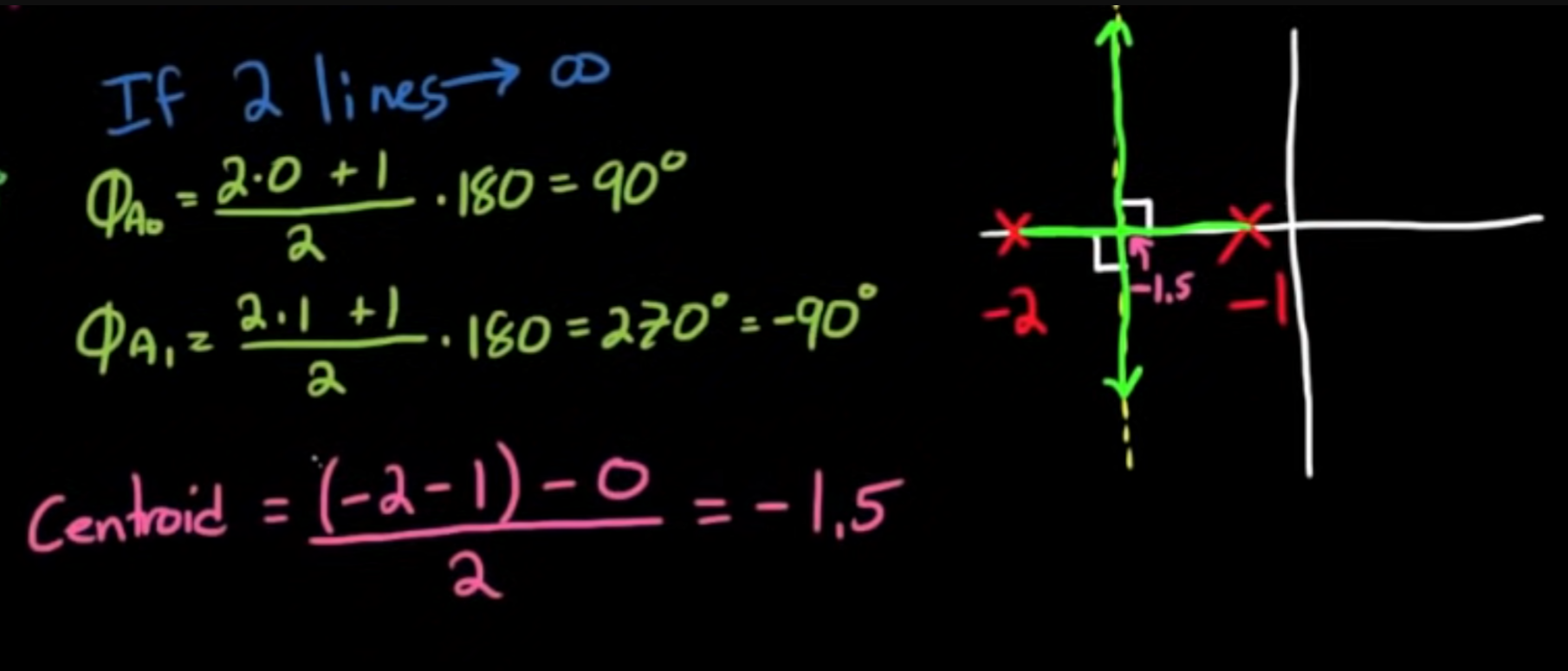
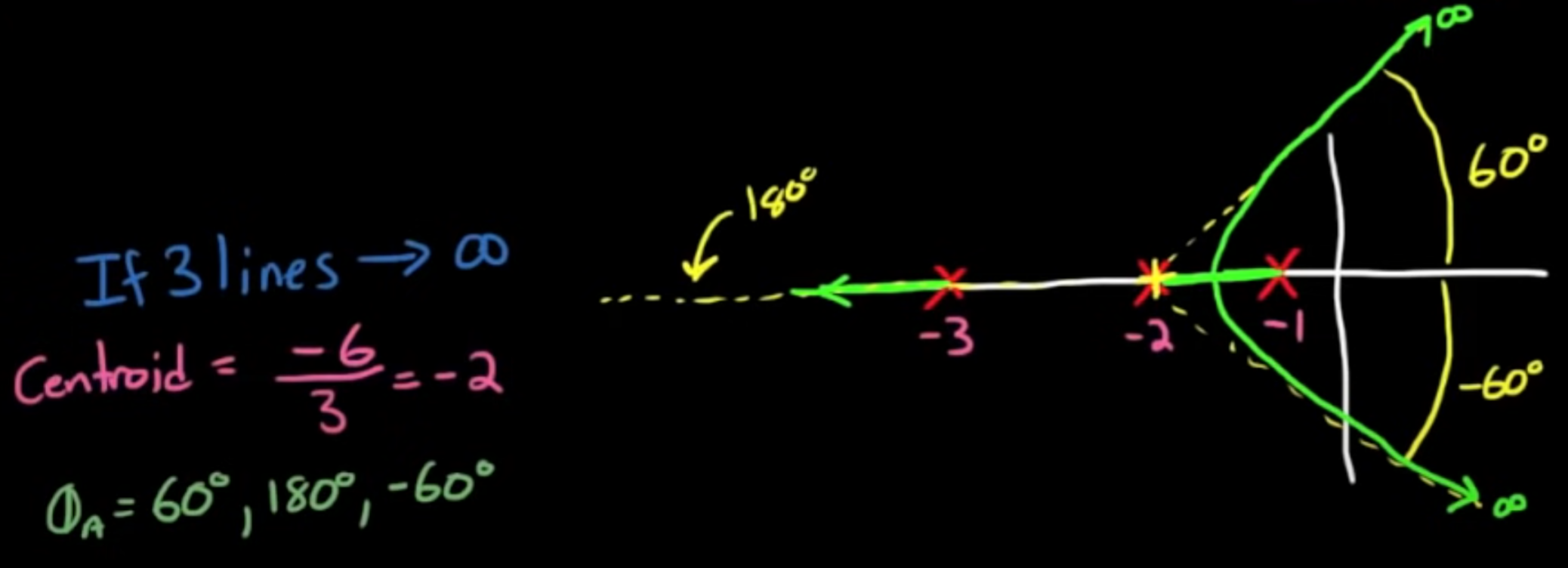
Angle of Asymptotes

$${\varphi }_A=\frac{2q+1}{n-m}\ast 180^o$$

Where: $n$ = # of poles $m$ = # of zeros

Centroid of Asymptotes

$$\frac{{\Sigma }_{\text{ finite poles}}-{\Sigma }_{\text{ finite zeros}}}{n-m}$$

Examples:

1 Line $⟶\infty$

2 Lines $⟶\infty$

3 Lines $⟶\infty$

Rule 9

If there are two lines to infinity the sum of all roots is constant

Rule 10: $0⟶-\infty$

Reverse Rule 5, and add $180^o$ to asymptote angles

Dump

Examples

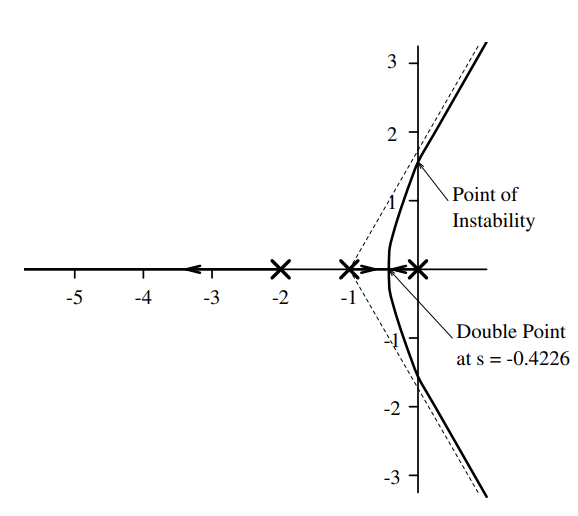
Question

Consider the System: $G(s)=\frac{K}{s(s+1)(s+2)}$ Draw the resulting root locus

Solution

• Draw the poles ($s=0,s=-1,s=-2$ ) and zeros (there are none here)
• Relative Order (poles - zeros), $n-m=3$ $\Rightarrow \text{3 asymptotes at: }-180^o,\text{and}\pm 60^o$
• Centroid at $X=\frac{(0-1-2)-(0)}{3}=-1$
• Double Point found at $\frac{d{G}_o}{ds}=0$, thus $\frac{d{G}_o}{ds}=\frac{d}{ds}(\frac{K}{s(s+1)(s+2)})=\frac{K(3s^2+6s+2)}{(s(s+1)(s+2){)}^2}=0\Rightarrow 3s^2+6s+2=0\Rightarrow s=-1\pm \frac{1}{\sqrt{3}}$
• Analyse root locus, as $-1-\frac{1}{\sqrt{3}}$ cannot be on the graph, we know the double point is at:$-1+\frac{1}{\sqrt{3}}=-0.4226$ Final Graph: