Second Order Systems

General Form

$$\ddot{x}(t)+2\xi {\omega }_n\dot{x}(t)+({\omega }_n{)}^{2}x(t)=Ku(t)$$

Where:

$\xi \to$ damping ratio, ${\omega }_n\to$ natural frequency $x(t)\to$ state || output, $u(t)\to$ input $K\to$ gain $t\to \infty ,\frac{x(t)}{u(t)}\to \frac{K}{{\omega }_n^2}$

In addition to this we can define the:

Damped Natural Frequency

${\omega }_d={\omega }_n\sqrt{1-{\xi }^2}$

From which we can also define the:

Period of Oscillation

${\tau }_d=\frac{2\pi }{{\omega }_d}$

Response:

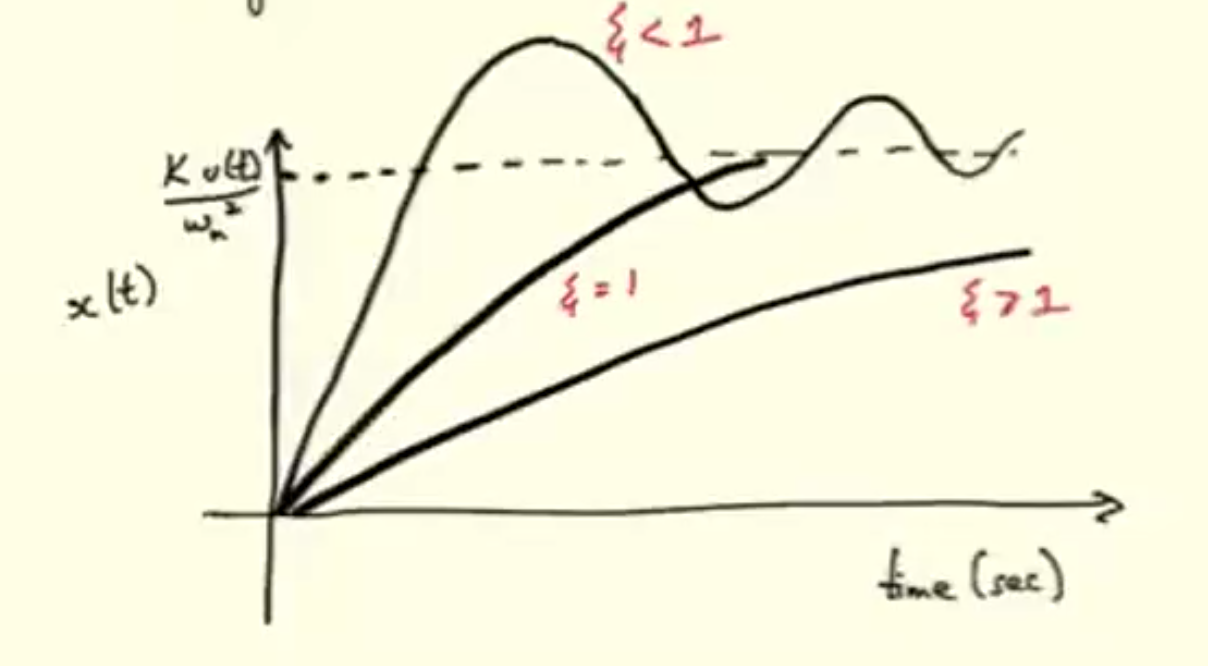
When our $\xi$ term is less than 1 we can call the system underdamped and when the $\xi$ term is larger than 1 it is overdamped. Finally when a system has exactly $\xi ==1$ then we can call it critically damped.

Abstract

We can visually distinguish the different systems as such:

Underdamped: Oscillations present, fastest approach to SS value, but overshoots and compensates

Critically Damped: The value at which we approach the SS value fastest without overshooting and therefore oscillating

Overdamped: All other states of the system where oscillations are not present however the SS value is not achieved in optimal time

Laplace:

$$\frac{C(s)}{R(s)}=\frac{{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}$$

Proportional Control

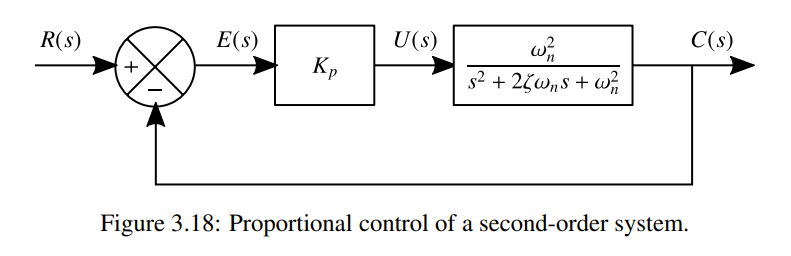
As we can see our controller ($G_1(s)=K_p$) and our plant ($G_2(s)=\frac{{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}$) create a proportional control system.

Reducing this block diagram we get:

$$\begin{array}{rl}\frac{C(s)}{R(s)}& =\frac{\frac{K_p{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}}{1+\frac{K_p{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}}=\frac{K_p{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2+K_p{\omega }_n^2}\\ \text{Given: }R(s)& =\frac{1}{s},\text{ it follows that}\\ C(s)& =\frac{K_p{\omega }_n^2}{s(s^2+2\xi {\omega }_{n}s+{\omega }_n^2+K_p{\omega }_n^2)}\\ c_{ss}& =\underset{s\to 0}{\lim }\{sC(s)\}=\underset{s\to 0}{\lim }\{\frac{K_p{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2+K_p{\omega }_n^2}\}\\ \therefore c_{ss}& =\frac{K_p{\omega }_n^2}{{\omega }_n^2(1+K_p)}=\frac{K_p}{1+K_p}\end{array}$$

Under similar logic:

$$\begin{array}{rl}{e}_{ss}& =\underset{s\to 0}{\lim }\{\frac{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2+K_p{\omega }_n^2}\}\\ e_{ss}& =\frac{1}{K_p+1}\end{array}$$

From this, expanding out full laplace equations we finally get the natural damped frequency ${\omega }_d$ for the closed loop system

$${\omega }_{d,cl}={\omega }_n\sqrt{K_p+1-{\xi }^2}$$

This means that simply increasing the proportional controller $K_p$ like we did in the first order system would cause the oscillations of the system to increase significantly. $K_p$ has NO effect on the damping

In these systems, increasing $K_p$ decreases the SS error, while increasing the frequency of oscillations:

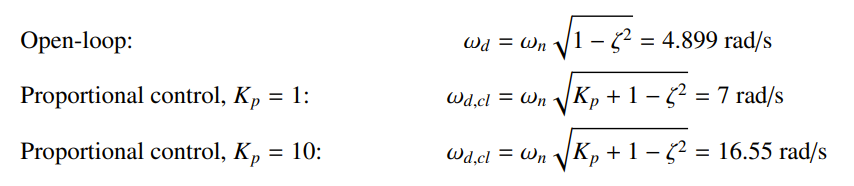
PD Control

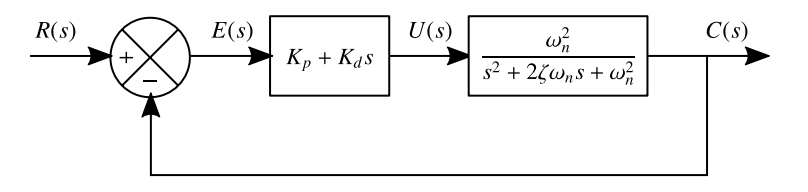As we can see our controller ($G_1(s)=K_p$) and our plant ($G_2(s)=\frac{{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}$) create a proportional control system.

The maths for $e_{ss}$ and $c_{ss}$ simplify much in the same way, so this will be skipped, however:

$$\begin{array}{rlr}{\omega }_{n,cl}& ={\omega }_n\sqrt{K_p+1}& {\xi }_{cl}=\frac{\xi +\frac{1}{2}{K}_d{\omega }_n}{\sqrt{K_p+1}}\\ {\omega }_{d,cl}& ={\omega }_{n,cl}\sqrt{1-{\xi }_{cl}^2}& \end{array}$$

The proportional control increases our frequency, but the derivate action modifies the damping of the system

So therefore in addition to scaling our final output by $\frac{K_p}{K_p+1}$ , there is an increase in oscillations over the open loop response:

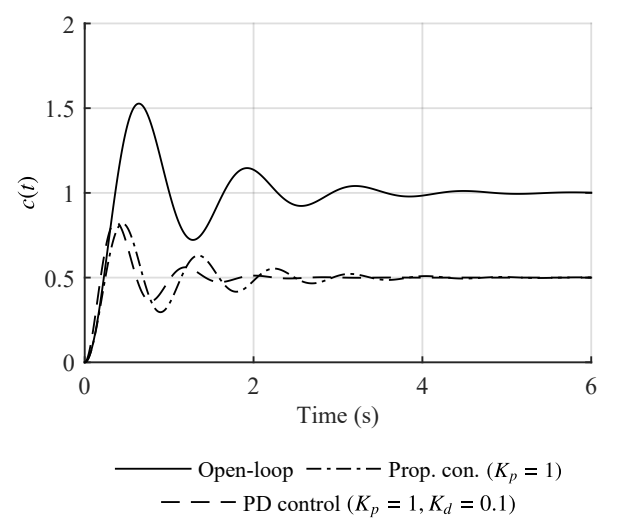
Underdamped Systems:

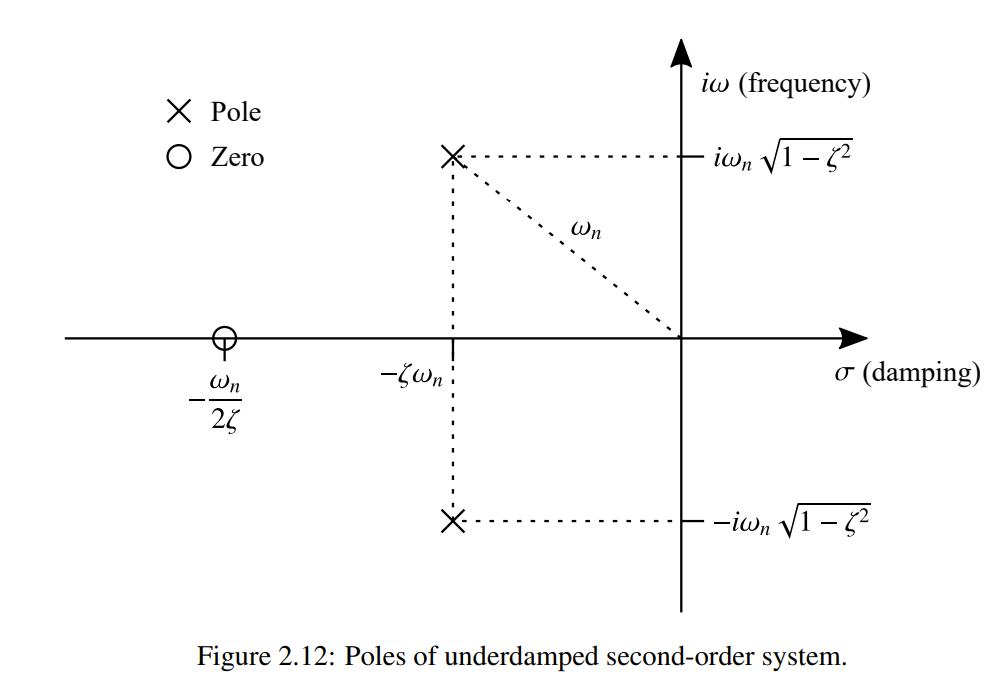
Roots and Zeros