- Q1: - 1a) - 1b) - 1c) - 1d)
- Q2 - 2a) - 2b) - 2c)
- Q3 - 3a) - 3ai) - 3aii) - 3aiii) - 3aiv) - 3av) - 3b)
- Q4 - 4a) - 4ai) - 4aii) - 4aiii) - 4b) - 4bi) - 4bii) - 4biii)
Q1:
1a)
Question
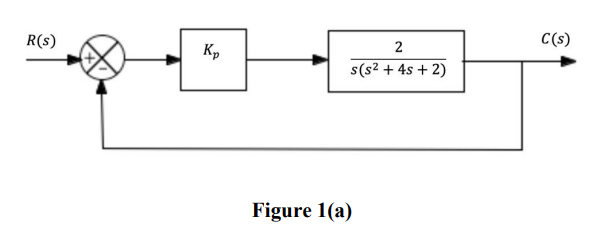
Figure 1(a) shows a unit feedback control system consisting of a proportional controller and a third-order plant. Find the range of proportional gain for which this system is stable. (5)
Answer
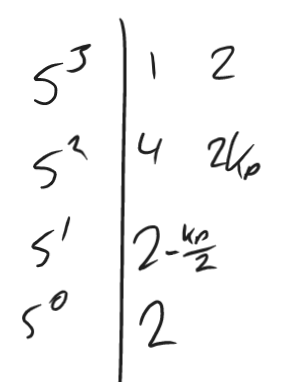
Characteristic:
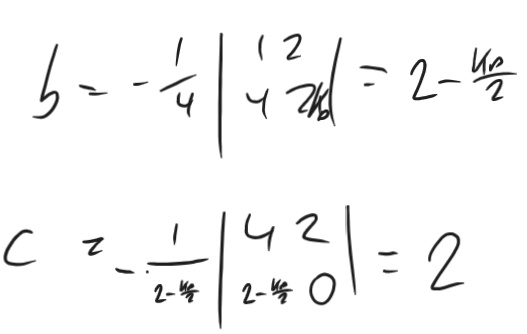
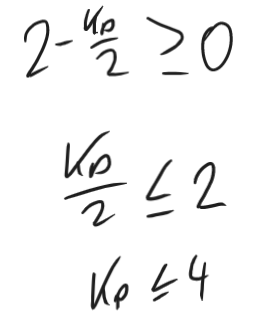
1b)
Question
Find the time domain response to a unit impulse input for the following second order system,
Solution
\begin{align} G(s) &= \frac{s+1}{s^2+5s+6} * \frac{1}{s} \\ &= \frac{s+1}{s(s+2)(s+3)} \\ \end{align} \begin{align} \frac{s+1}{s(s+2)(s+3)} &= \frac{1}{(s+2)(s+3)} + \frac{1}{s(s+2)(s+3)} \\ \frac{1}{s(s+2)(s+3)} &= \frac As + \frac B{s+2} + \frac C{s+3} \\ 1&= A(s+2)(s+3) + Bs(s+3)+Cs(s+2) \\ 1&= (A+B+C)s^2 + (5A+3B+2C)s + 6A\\ s^0 &: 1 = 6A, \quad A =\frac{1}{6} \\ s^1 &: 0 = 5A+3B+2C, \quad3B+2C =-\frac{5}{6} \\ s^2 &: 0=A+B+C, \quad B+C=-\frac{1}{6} \\ \therefore B &= -\frac{3}{6} = -\frac 12 \\ \therefore C &= \frac 26 = \frac 13 \\ \frac{1}{s(s+2)(s+3)} &= \frac{0.1667}{s} - \frac{0.5}{s+2} + \frac{0.333}{s+3} \\ \frac{1}{(s+2)(s+3)} & = \frac{D}{s+2} + \frac{E}{s+3} \\ 1 & = D(s+3) + E(s+2) \\ 1& = (D+E)s + (3D+2E) \\ \therefore & \quad E = -D, \quad 3D + 2E =1 \\ \rightarrow & \quad D =1, \quad E = -1 \\ \frac{1}{(s+2)(s+3)} & = \frac{1}{s+2} - \frac{1}{s+3} \\ G(s) &= \frac{0.1667}{s} + \frac{0.5}{s+2} - \frac{0.66667}{s+3} \\ \Rightarrow g(t) &= \frac{t}{6} + \frac{e^{-2t}}{2} - \frac{2e^{-3t}}{3} \end{align}
1c)
Question
Figure 1(c) shows the block diagram for a feedback control system with a second order plant and a PD controller. Sketch the pole-zero plot and hence comment on the stability and response characteristics of the system, given:
Solution
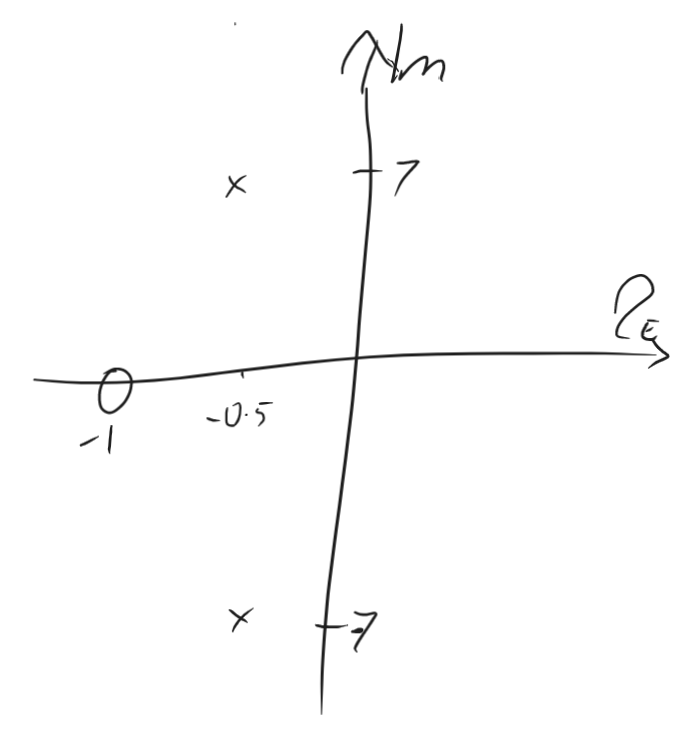 This system is stable, and the response would be oscillatory for all
This system is stable, and the response would be oscillatory for all
1d)
Question
A PD controller with proportional gain 𝐾𝑝 and derivative gain 𝐾𝑑 is in series with a plant with the transfer function: and employs a unity negative feedback loop. Find suitable values for 𝐾𝑝 and 𝐾𝑑 so that the closed-loop system has a settling time of 3 sec and a peak time of 1 sec.
Solution
Q2
Question
The vertical motion of a service lift is controlled by means of lifting cables. The desired position is given by and the actual position is given by ℎ(𝑠). The error between actual and desired position is amplified and used to actuate the lifting cables. The actual position is measured and fed back by a sensor which has unity gain. and are the transfer functions of the controller and plant respectively.
2a)
Question
A unit step input is provided. If only proportional control is used, find the timedomain response and show that the position of the lift oscillates about the reference value of 1. Find the period of this oscillation.
Solution
\begin{align} \frac{h(s)}{h_r(s)} &= \frac{\frac{K}{s^2}}{1+\frac{K}{s^2}} = \frac{K}{s^2+K} \\ \text{Given} & \text{ that }h_r(s) = \frac{1}{s}\text{:} \\ h(s) &= \frac{K}{s(s^2+K)} \\ \Rightarrow h_{ss} &= \lim_{s\rightarrow0}\{sh(s)\} = \lim_{s\rightarrow0}\{\frac{K}{s^2+K}\} = 1 \\ \frac{1}{s(s^2+K)} &= \frac{A}{s} + \frac{Bs+C}{s^2+K} \\ 1 &=A(s^2+K) + s(Bs+C) \\ 1 &= (A+B) s^2 + Cs +KA \\ s^0&: 1=KA, \quad A =\frac{1}{K} \\ s^1&: 0= C \\ s^2&:0=A+B, \quad B=-\frac{1}{K} \\ \frac{1}{s(s^2+K)} &= \frac{1}{K}*\frac{1}{s} -\frac{1}{K}+\frac{s}{s^2+K} \\ h(s) &=\frac{1}{s} - \frac{s}{s^2+K} \\ \Rightarrow h(t) &=1-\cos (Kt) \end{align} Period = (Whole cos takes to complete )
2b)
Question
Show that the addition of derivative action to the system can ensure a non-oscillatory response. Find a relation between the derivative and proportional gains that ensures the response is non-oscillatory.
Solution
\begin{align} \\ \frac{h(s)}{h_r(s)} &= \frac{K_ds+K_p}{s^2+K_ds+K_p} \\ K_d&=2\xi\omega_n , \quad K_p =\omega_n^2 \\ \xi &= \frac{K_d}{2\sqrt{K_p}} \\ \text{No }&\text{Oscillations at }\xi\geq1 \\ \rightarrow&\quad \frac{K_d}{2\sqrt{K_p}}\geq1 \\ \Rightarrow& \quad K_d \geq2\sqrt{K_p} \end{align}
2c)
Question
When the proportional and derivative gains are set to 𝐾𝑝 = 16 and 𝐾𝑑 = 8, respectively, find the damping ratio and natural frequency of the system. Derive the time-domain response of the lift for a unit step input and confirm that it is not oscillatory.
Solution
\begin{align} h(s) &=\frac{8s+16}{s(s^2+8s+16)} = \frac{8s+16}{s(s+4)^2} \\ \frac{1}{s(s+4)^2} &= \frac As + \frac{B}{s+4} + \frac{C}{(s+4)^2} \\ 1 &= (s+4)^2A + s(s+4) B + sC \\ 1 &= (s^2+8s+16)A + (s^2+4s)B+ s)C \\ 1 &= (A+B)s^2 + (4B+8A+C)s + 16A \\ s^0 &: 16 = 16A, \quad A=1 \\ s^1 &: 8 = 8A +4B+C, \quad 4B+C = 0 \\ s^2&: 0=A+B, \quad B=-1,C= 4\\ h(s)&= \frac{1}{s}-\frac1{s+4}+\frac{4}{(s+4)^2} \\ \Rightarrow h(t) &= 1 - e^{-4t}+ \sin(4t) \end{align}
?????? I messed up :(
Q3
Question
A control system regulates a process which has the transfer function A controller with transfer function 𝐶(𝑠) us used in a negative feedback configuration and generates a control signal which is the input to 𝑃(𝑠).
3a)
Question
Perform a root locus analysis, for varying 𝐾 > 0, for a proportional controller, i.e. 𝐶(𝑠) = 𝐾 by following these steps:
3ai)
Question
Determine the open loop transfer function 𝐺𝑜(𝑠) = 𝐶(𝑠)𝑃(𝑠), and identify the open-loop poles and open-loop zeros of the system.
Solution
Zeros at -6 Poles at -3,-5,-10
3aii)
Question
Determine the number of asymptotes of the root locus and where they meet. Calculate the location of any double point(s).
Solution
Double point at
3aiii)
Question
Sketch the root-locus for this system, using the information derived in (i)–(ii).
Solution
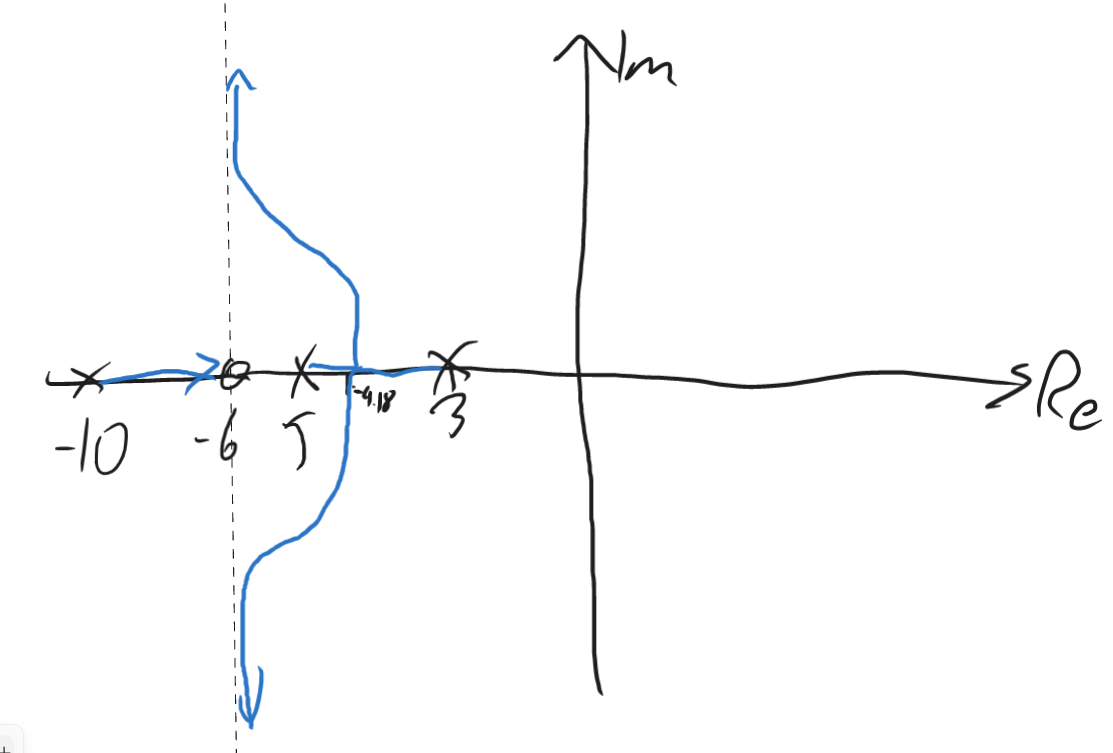
3aiv)
Question
Discuss the characteristics of the closed loop system for different values of 𝐾, i.e. for small 𝐾 and for larger values of 𝐾. Does the closed loop system become unstable for any value of 𝐾?
Solution
The system never become unstable for any . The system becomes oscillatory for larger , but remains stable
3av)
?
3b)
Question
The proportional controller is now replaced by an integral controller, i.e. Apply this controller to the plant 𝑃𝑃(𝑠𝑠) given above. Determine the number of asymptotes of the root locus and where they meet. Assuming that the double point in this case is at −1.31, sketch the root locus diagram. Discuss the differences to the diagram which you obtained in (a) and the characteristics of the closed loop system for different values of 𝐾.
Solution
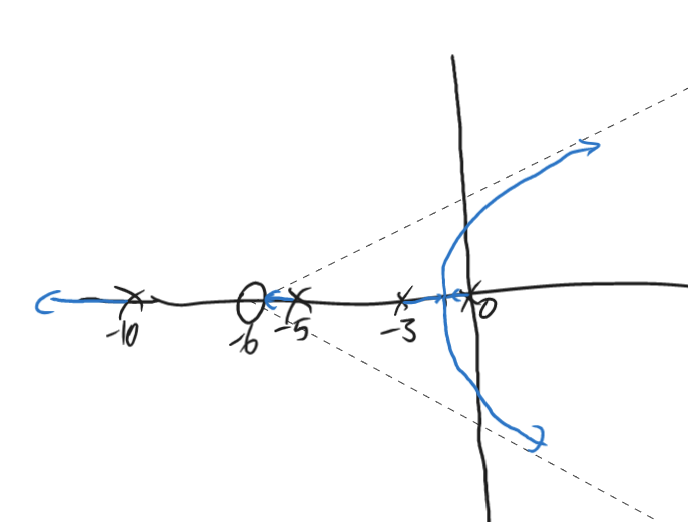 This system can become unstable, for large values of , it also becomes oscillatory for a smaller value of as to before
This system can become unstable, for large values of , it also becomes oscillatory for a smaller value of as to before
Q4
4a)
Question
The Nyquist stability criterion can be used to determine the stability of a closed loop feedback system, based on the frequency response of the open-loop system.
4ai)
Question
What are the two stability margins which can be derived from the frequency response of an open-loop system? What is their significance.
Solution
Gain Margin - How much you are able to increase your gain before your system becomes unstable Phase Margin - How much delay the phase of the system can have beefore the system becomes unstable
4aii)
Question
Sketch a typical Nyquist plot and indicate these two margins
Solution
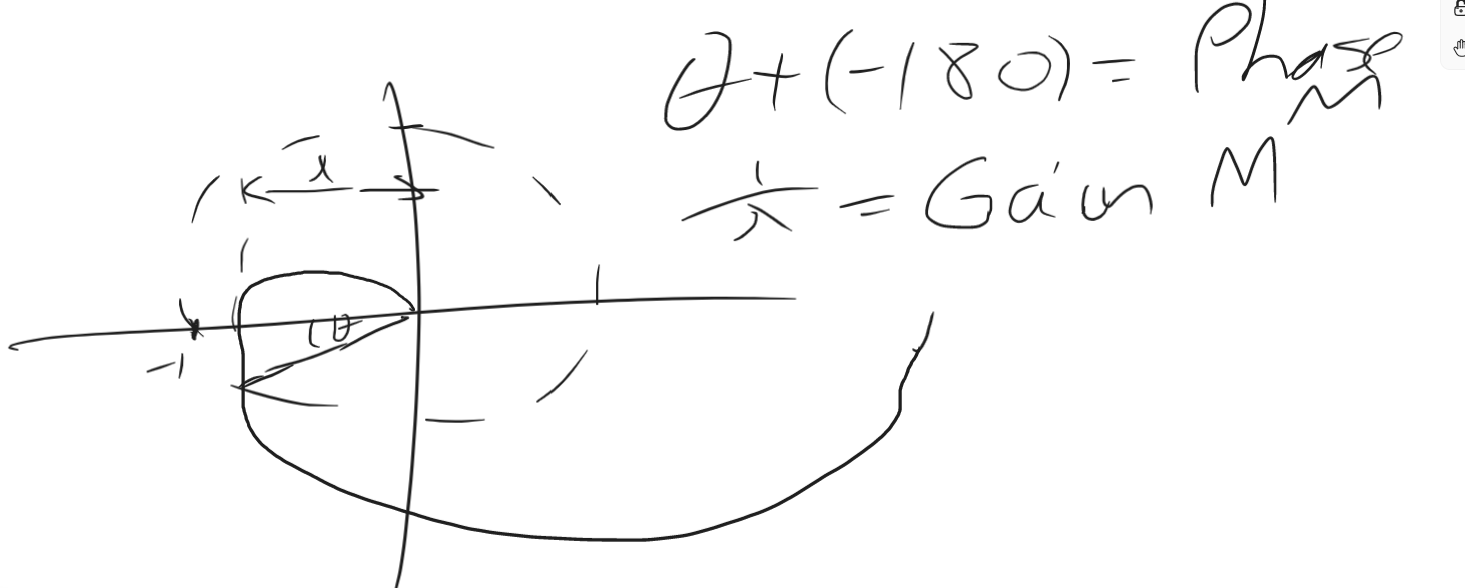
4aiii)
Question
How can these stability margins be determined from a Bode diagram?
Solution
The gain margin is the magnitude (dB) the system is at when the system reaches phase on the bode
The phase margin is the difference from -180 to the actual phase achieved at
4b)
Question
Consider the open loop system:
4bi)
Question
Derive an expression for the frequency response for this system. What is the steady state open-loop gain of this system in dB?
Solution
dB
4bii)
Question
Sketch the approximate Bode diagram for the system in (a), clearly showing the asymptotes and corner frequencies. In the diagram, indicate the stability margins of the corresponding closed loop system. Briefly discuss what the values of these margins mean for the stability of the closed loop system.
Solution
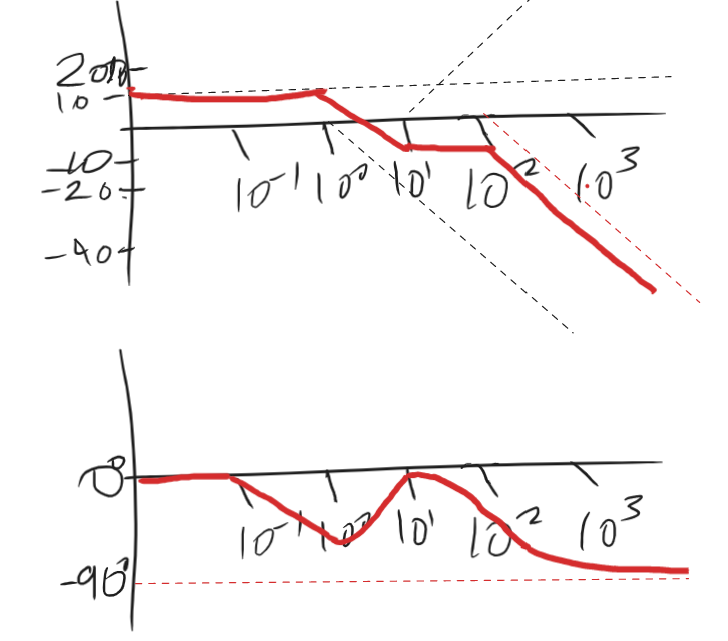 Phase Margin , this means we can manage up to 135 degrees of phase shift before the system becomes unstable.
Gain Margin , as we never reach
This means the system is stable for all
Phase Margin , this means we can manage up to 135 degrees of phase shift before the system becomes unstable.
Gain Margin , as we never reach
This means the system is stable for all
4biii)
Question
Explain how the Bode diagram changes for the system from (c) with an additional gain of 𝐾 = 10, i.e. for . Sketch the Bode diagram of the modified system and comment on changes of the stability margins.
Soltuion
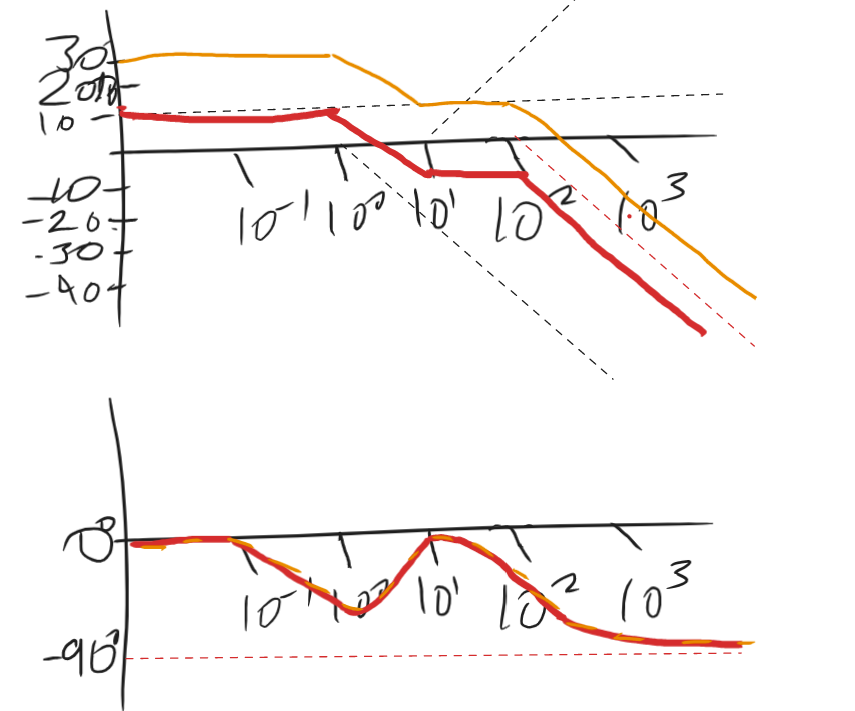 No changes are observed for either the Gain Margin, which still doesn’t exist, and the phase plot shows no changes, meaning the Phase Margin has not changed either.
No changes are observed for either the Gain Margin, which still doesn’t exist, and the phase plot shows no changes, meaning the Phase Margin has not changed either.